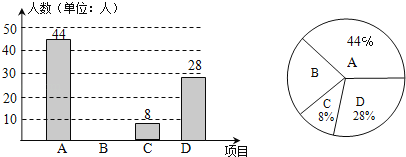
题目内容
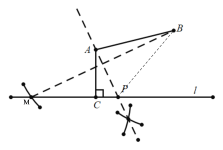
【题目】(1)如图1,已知AC⊥直线l,垂足为C.请用直尺(不含刻度)和圆规在直线l上求作一点P(不与点C重合),使PA平分∠BPC;
(2)如图2,在(1)的条件下,若![]() ,AC=
,AC=![]() ,作BD⊥直线l,垂足为D,则BD= .
,作BD⊥直线l,垂足为D,则BD= .
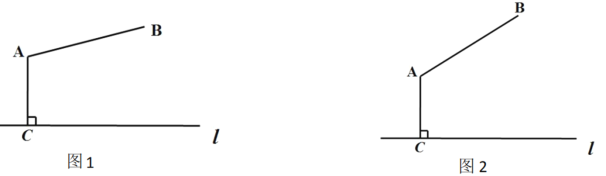
【答案】(1)见解析;(2)2![]() .
.
【解析】
(1)以A为圆心,AB为半径画圆,与直线l相交于M,连接AM,分别以B、M为圆心,大于BM的一半为半径画弧,交于一点,作经过该点和点A的直线与l交于一点,即为P点;
(2)当![]() 时,M、A、B在同一直线上,得出AC是三角形MBD的中位线,从而求解.
时,M、A、B在同一直线上,得出AC是三角形MBD的中位线,从而求解.
(1)以A为圆心,AB为半径画圆,与直线l相交于M,连接AM,分别以B、M为圆心,大于BM的一半为半径画弧,交于一点,作经过该点和点A的直线与l交于一点,即为P点如图所示;
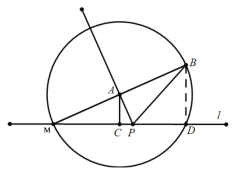
(2)当![]() 时,M、A、B在同一直线上
时,M、A、B在同一直线上
∵A是BM中点,![]()
∴AC是三角形MBD的中位线
∴![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目