题目内容
如图所示,某地有一座圆弧形的拱桥,桥下水面宽为12米,拱顶高出水面4米.
(1)求这座拱桥所在圆的半径.
(2)现有一艘宽5米,船舱顶部为正方形并高出水面3.6米的货船要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.

(1)求这座拱桥所在圆的半径.
(2)现有一艘宽5米,船舱顶部为正方形并高出水面3.6米的货船要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.

(1)连接OA,
根据题意得:CD=4米,AB=12米,
则AD=
AB=6(米),
设这座拱桥所在圆的半径为x米,
则OA=OC=x米,OD=OC-CD=(x-4)米,
在Rt△AOD中,OA2=OD2+AD2,
则x2=(x-4)2+62,
解得:x=6.5,
故这座拱桥所在圆的半径为6.5米.
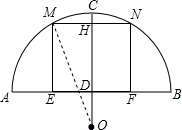 (2)货船不能顺利通过这座拱桥.理由:
(2)货船不能顺利通过这座拱桥.理由:
连接OM,
设MN=5米,
∵OC⊥MN,
∴MH=
MN=2.5(米),
在Rt△OMH中,OH=
=6(米),
∵OD=OC-CD=6.5-4=2.5(米)
∵OH-OD=6-2.5=3.5(米)<3.6米,
∴货船不能顺利通过这座拱桥.

根据题意得:CD=4米,AB=12米,
则AD=
| 1 |
| 2 |
设这座拱桥所在圆的半径为x米,
则OA=OC=x米,OD=OC-CD=(x-4)米,
在Rt△AOD中,OA2=OD2+AD2,
则x2=(x-4)2+62,
解得:x=6.5,
故这座拱桥所在圆的半径为6.5米.
 (2)货船不能顺利通过这座拱桥.理由:
(2)货船不能顺利通过这座拱桥.理由:连接OM,
设MN=5米,
∵OC⊥MN,
∴MH=
| 1 |
| 2 |
在Rt△OMH中,OH=
| OM2-MH2 |
∵OD=OC-CD=6.5-4=2.5(米)
∵OH-OD=6-2.5=3.5(米)<3.6米,
∴货船不能顺利通过这座拱桥.


练习册系列答案
相关题目

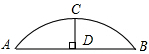

 试问:(1)中的结论是否成立?并说明理由.
试问:(1)中的结论是否成立?并说明理由.


