题目内容
【题目】在![]() 中,
中,![]() ,在
,在![]() 的外部作等边三角形
的外部作等边三角形![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() .
.
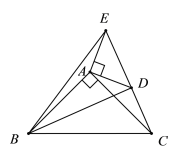
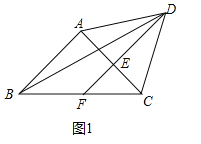
(1)如图1,若![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
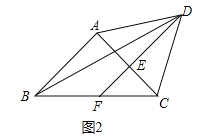
①补全图2;
②若![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ;(2)①补全图形,如图所示.见解析;②见解析.
;(2)①补全图形,如图所示.见解析;②见解析.
【解析】
(1)分别求出∠ADF,∠ADB,根据∠BDF=∠ADF-∠ADB计算即可;
(2)①根据要求画出图形即可;
②设∠ACM=∠BCM=α,由AB=AC,推出∠ABC=∠ACB=2α,可得∠NAC=∠NCA=α,∠DAN=60°+α,由△ABN≌△ADN(SSS),推出∠ABN=∠ADN=30°,∠BAN=∠DAN=60°+α,∠BAC=60°+2α,在△ABC中,根据∠BAC+∠ACB+∠ABC=180°,构建方程求出α,再证明∠MNB=∠MBN即可解决问题;
(1)解:如图1中,
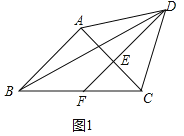
在等边三角形![]() 中,
中,
![]() ,
,![]() .
.
∵![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)①补全图形,如图所示.
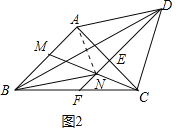
②证明:连接![]() .
.
∵![]() 平分
平分![]() ,
,
∴设![]() ,
,
∵![]() ,
,
∴![]() .
.
在等边三角形![]() 中,
中,
∵![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
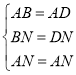
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目