题目内容
【题目】如图,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E在同一条直线上,连结BD,BE.以下四个结论:①BD=CE ;②BD⊥CE ;③∠ACE+∠DBC=45°; ④∠ACE=∠DBC ,其中结论正确的是____________
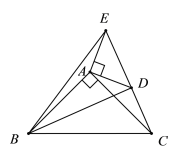
【答案】①②③
【解析】
①由AB=AC,AD=AE,利用等式的性质得到夹角相等,利用SAS得出△ABD≌△AEC,由全等三角形的对应边相等得到BD=CE;
②由△ABD≌△AEC得到一对角相等,再利用等腰直角三角形的性质及等量代换得到![]() ,从而得BD⊥CE;
,从而得BD⊥CE;
③由等腰直角三角形的性质得到∠ABD+∠DBC=45°,等量代换得到∠ACE+∠DBC=45°;
④由△ABD≌△AEC得到![]() ,而
,而![]() 与
与![]() 不一定相等,从而说明④错误.
不一定相等,从而说明④错误.
∵∠BAC=∠DAE=90°,AB=AC,AD=AE,
∴![]()
![]()
![]()
![]()
在![]() 与
与![]() 中
中
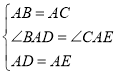
![]()
![]() ,①正确
,①正确
∵![]()
∴![]()
![]()
![]() ,②正确
,②正确
∵![]()
∴![]()
![]() ,③正确
,③正确
∵![]()
∴![]()
而![]() 与
与![]() 不一定相等,
不一定相等,
∴![]() 与
与![]() 也不一定相等,④错误
也不一定相等,④错误
综上:①②③正确.
故答案为:①②③.

练习册系列答案
相关题目