题目内容
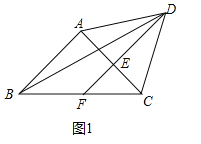
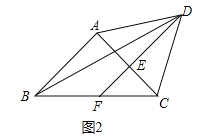
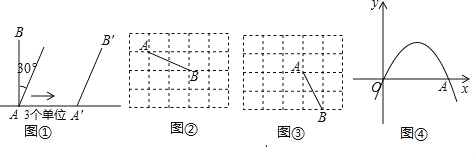
【题目】定义：以线段l的一个端点为旋转中心，将这条线段顺时针旋转α（0°＜α≤360°），再沿水平方向向右平移m个单位后得到对应线段l′（若m＜0，则表示沿水平向左的方向平移|m|个单位），则将线段l到线段l′的变换记为＜α，m＞．如图①，将线段AB绕点A顺时针旋转30°，再沿水平向右的方向平移3个单位后得到线段A′B′的变换记为＜30°，3＞．
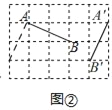
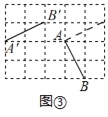
（1）已知：图②、图③均为5×4的正方形网格，在图②中将线段AB绕点A进行变换＜90°，4＞，得到对应线段A′B′；在图③中将线段AB绕点A进行变换＜270°，﹣3＞，得到对应线段A′B′，按要求分别画出变换后的对应线段．
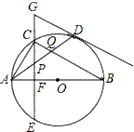
（2）如图④，在平面直角坐标系中，抛物线y=﹣
x2+2x与x轴正半轴交于点A，线段OA绕点A进行变换＜α，m＞后得到对应线段的一个端点恰好落在抛物线的顶点处，直接写出符合题意的＜α，m＞为________________________________．
【答案】（1）作图见解析；（2）＜30°，
＞或＜150°，
＞．
【解析】
利用新定义直接作出图形；
先确定出点A的坐标，抛物线的顶点坐标，再判断出线段OA绕点A顺时针旋转使点O的对应点落在直线l上，分两种情况分别讨论求得
（1）①如图②所示，A'B'为所求作的线段，
②如图③所示，A'B'为所求作的线段，
（2）
∴此抛物线的顶点E坐标为（2，2），
∴x=0或x=4，
∴A（4，0），
∴OA=4，
过E作直线l∥x轴，
由平移知，OA绕点A顺时针旋转，点O的对应点落在直线l上，如图④中点D或F，
①当点O的对应点落在D点时，过点D作DP⊥x轴，
∴DP=2，
在Rt△APD中，AD=OA=4，
∴＜α，m＞为＜30°，＞，
②当点O的对应点落在点F处时，
同①的方法得，＜α，m＞为＜150°，＞，
故答案为＜30°，＞或＜150°，＞．
