��Ŀ����
����Ŀ��ijУ�����꼶�����꼶��չ���Ķ���ѧ����֪ʶ��������У�ߡ����꼶����ѧ��400�ˣ��������ȡ20��ѧ�������˳������飬���������֪ʶ�����ɼ�����λ���֣����������ݽ��������������ͷ�������������˲�����Ϣ��
a�����꼶ѧ��֪ʶ�����ɼ���ƽ��������λ���������������ʣ�80�ּ����ϣ����±���ʾ��
�꼶 | ƽ���� | ��λ�� | ���� | ������ |
���꼶 | 84. 2 | 77 | 74 | 45�� |
b�����꼶ѧ��֪ʶ�����ɼ�������ͳ��ͼ���£����ݷ�Ϊ5�飬A��50��x��59�� B��60��x��69��C��70��x��79��D��80��x��89��E��90��x��100��
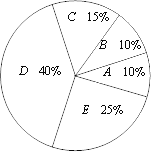
c�����꼶ѧ��֪ʶ�����ɼ���D����ǣ�87 88 88 88 89 89 89 89
����������Ϣ���ش��������⣺
��1�����꼶ѧ��֪ʶ�����ɼ�����λ���� �֣�
��2��������Ƹ�У�ߡ����꼶����ѧ���дﵽ�����㡱���ж����ˣ�
��3�����н��ۣ��ٰ��꼶�ɼ���������89�֣��ڰ��꼶�ɼ���ƽ��������Ϊ86�֣��۰��꼶�ɼ��ļ������Ϊ50�֣�����������ȷ���۵������ ��
���𰸡���1��88����2��440����3����
��������
��1���ҵ�20��ѧ�����꼶ѧ��֪ʶ�����ɼ����ڵ�10��11���ķ���������⣻
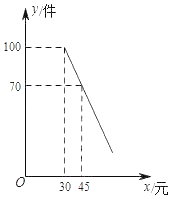
��2�����ߡ����꼶�����������������ʼ�����⣻
��3������������ƽ����������Ķ��弴�������ж�.
��1��������ɵ�20��ѧ�����꼶ѧ��֪ʶ�����ɼ����ڵ�10��11���ķ����ֱ�Ϊ88��88��
����λ����88�֣�
���88.
��2��400��45%��400����40%��25%����180��260��440�ˣ�
�𣺹��Ƹ�У�ߡ����꼶����ѧ���дﵽ������������440��
��3����20�����꼶�ɼ���������89�֣�����ȫ����꼶�ɼ���������һ����89�֣��ʴ��ڰ��꼶���������ݲ�ȫ���ʲ������ƽ�������ʴ���
�������꼶�ɼ���СΪ50�֣����Ϊ100��ʱ������Ϊ50�֣�����ȷ��
��������

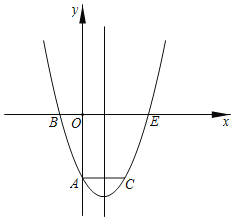
����Ŀ�����κ���y��ax2+bx+c��a��b��cΪ��������a��0���е�x��y�IJ��ֶ�Ӧֵ�����
x | ��1 | 0 | 1 | 3 |
y | ��1 | 3 | 5 | 3 |
���н��۴�����ǣ�������
A.ac��0
B.��x��1ʱ��y��ֵ��x���������С
C.3�Ƿ���ax2+��b��1��x+c��0��һ����
D.����1��x��3ʱ��ax2+��b��1��x+c��0