题目内容
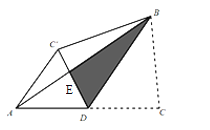
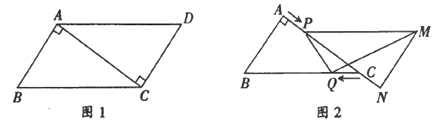
【题目】如图1,在平行四边形ABCD中,AB=3cm, BC=5cm, ![]() ,
, ![]() 沿 AC的方向匀速平移得到
沿 AC的方向匀速平移得到![]() ,速度为1 cm/ s;同时,点Q从点C出发,沿CB方向匀速移动,速度为1cm/s,当
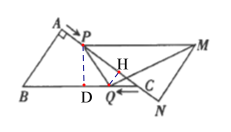
,速度为1 cm/ s;同时,点Q从点C出发,沿CB方向匀速移动,速度为1cm/s,当![]() 停止平移时,点Q也停止移动,如图2,设移动时间为t(s)(0< <4),连结PQ,MQ ,
停止平移时,点Q也停止移动,如图2,设移动时间为t(s)(0< <4),连结PQ,MQ ,
解答下列问题:
(1)当t为何值时,![]() ?
?
(2)当t为何值时,![]() ?
?
(3)当t为何值时,![]() ?
?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由题意得:AP=t,CQ=t,CP=4-t,当![]() 时,则AB∥PQ,得到:
时,则AB∥PQ,得到:![]() ,即可求解;
,即可求解;
(2)过点Q作QH⊥AC于点H,易证:CQH~CBA,得QH=![]() ,CH=
,CH=![]() ,PH=4-
,PH=4-![]() ,当
,当![]() 时,则PQH为等腰直角三角形,列出方程,即可求解;
时,则PQH为等腰直角三角形,列出方程,即可求解;
(3)过点P作PD⊥BC,易证:PQD~ MPQ,得:![]() ,由PDC~BAC,得
,由PDC~BAC,得![]() ,
,![]() ,DQ =
,DQ =![]() ,结合
,结合![]() ,列出方程,即可求解.
,列出方程,即可求解.
(1)∵AB=3cm, BC=5cm, ![]() ,
,
∴AC=![]() ,
,
由题意得:AP=t,CQ=t,CP=4-t,
∵AB∥MN,
∴当![]() 时,则AB∥PQ,
时,则AB∥PQ,
∴![]() ,即:
,即:![]() ,解得:t=
,解得:t=![]() ;
;
∴当t =![]() 时,
时,![]() ;
;
(2)过点Q作QH⊥AC于点H,
∴QH∥BA,
∴CQH~CBA,
∴CQ:QH:CH=CB:BA:CA=5:3:4,
∴QH=![]() ,CH=
,CH=![]() ,
,
∴PH=4-t-![]() =4-
=4-![]() ,
,
当![]() 时,则PQH为等腰直角三角形,
时,则PQH为等腰直角三角形,
∴PH=QH,即:![]() =4-
=4-![]() ,解得:t=
,解得:t=![]() ,
,
∴当t=![]() 时,
时,![]() ;
;
(3)过点P作PD⊥BC,
若![]() ,则∠PQM=∠PDQ,
,则∠PQM=∠PDQ,
∵PM∥BC,
∴∠MPQ=∠PQD,
∴PQD~ MPQ,
∴![]() ,
,
∴![]() ,
,
∴ ![]() .
.
∵∠PDC=∠BAC=90°,∠ACB=∠DCP,
∴PDC~BAC,
∴![]() ,即:
,即:![]() ,
,
解得:![]() ,
,![]() ,
,
∴DQ=CD-CQ=![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,![]() (舍去),
(舍去),
∴当t=![]() 时,
时,![]() .
.

【题目】某校在七年级、八年级开展了阅读文学名著知识竞赛.该校七、八年级各有学生400人,各随机抽取20名学生进行了抽样调查,获得了他们知识竞赛成绩(单位:分),并对数据进行整理、描述和分析.下面给出了部分信息.
a.七年级学生知识竞赛成绩的平均数、中位数、众数、优秀率(80分及以上)如下表所示:
年级 | 平均数 | 中位数 | 众数 | 优秀率 |
七年级 | 84. 2 | 77 | 74 | 45﹪ |
b.八年级学生知识竞赛成绩的扇形统计图如下(数据分为5组,A:50≤x≤59; B:60≤x≤69;C:70≤x≤79;D:80≤x≤89;E:90≤x≤100)
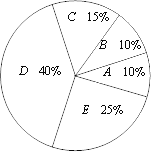
c.八年级学生知识竞赛成绩在D组的是:87 88 88 88 89 89 89 89
根据以上信息,回答下列问题:
(1)八年级学生知识竞赛成绩的中位数是 分;
(2)请你估计该校七、八年级所有学生中达到“优秀”的有多少人?
(3)下列结论:①八年级成绩的众数是89分;②八年级成绩的平均数可能为86分;③八年级成绩的极差可能为50分.其中所有正确结论的序号是 .