题目内容
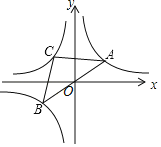
【题目】如图,抛物线y=ax2+bx+c经过点A(0,﹣3)、B(﹣1,0)、C(2,﹣3),抛物线与x轴的另一交点为点E,点P为抛物线上一动点,设点P的横坐标为t.
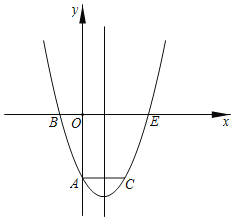
(1)求抛物线的解析式;
(2)若点P在第一象限,点M为抛物线对称轴上一点,当四边形MBEP恰好是平行四边形时,求点P的坐标;
(3)若点P在第四象限,连结PA、PE及AE,当t为何值时,△PAE的面积最大?最大面积是多少?
(4)是否存在点P,使△PAE为以AE为直角边的直角三角形,若存在,直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)y=x2﹣2x﹣3;(2)P(4,5);(3)当t=![]() 时,S有最大值
时,S有最大值![]() ;(4)存在,理由,点P的坐标为:(﹣2,5)或(1,﹣4)
;(4)存在,理由,点P的坐标为:(﹣2,5)或(1,﹣4)
【解析】
(1)抛物线y=ax2+bx+c经过点A(0,﹣3)、C(2,﹣3),则函数的对称轴为:x=1,故点E(3,0),即可求解;
(2)四边形MBEP恰好是平行四边形时,则MP=BE=3,故t=4,则点P(4,5);
(3)△PAE的面积S=![]() PH×OE=
PH×OE=![]() (t﹣3﹣t2+2t+3)=
(t﹣3﹣t2+2t+3)=![]() (﹣t2+3t),即可求解;
(﹣t2+3t),即可求解;
(4)分∠PEA=90°、∠PAE=90°两种情况,分别求解即可.
解:(1)抛物线y=ax2+bx+c经过点A(0,﹣3)、C(2,﹣3),则函数的对称轴为:x=1,
故点E(3,0),
抛物线表达式为:y=a(x﹣3)(x+1)=a(x2﹣2x﹣3),
故﹣3a=﹣3,解得:a=1,
故抛物线的表达式为:y=x2﹣2x﹣3…①;
(2)四边形MBEP恰好是平行四边形时,则MP=BE=4,
故t=4,则点P(4,5);
(3)过点C作y轴的平行线交AE于点H,
由点A、E的坐标得直线AE的表达式为:y=x﹣3,

设点P(t,t2﹣2t﹣3),则点H(t,t﹣3),
△PAE的面积S=![]() PH×OE=
PH×OE=![]() (t﹣3﹣t2+2t+3)=
(t﹣3﹣t2+2t+3)=![]() (﹣t2+3t),
(﹣t2+3t),
当t=![]() 时,S有最大值
时,S有最大值![]() ;
;
(4)直线AE表达式中的k值为1,则与之垂直的直线表达式中的k为﹣1.
①当∠PEA=90°时,
直线PE的表达式为:y=﹣x+b,经点E的坐标代入并解得:
直线PE的表达式为:y=﹣x+3…②,
联立①②并解得:x=﹣2或3(舍去3),
故点P(﹣2,5);
②当∠PAE=90°时,
同理可得:点P(1,﹣4);
综上,点P的坐标为:(﹣2,5)或(1,﹣4).

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】某校在七年级、八年级开展了阅读文学名著知识竞赛.该校七、八年级各有学生400人,各随机抽取20名学生进行了抽样调查,获得了他们知识竞赛成绩(单位:分),并对数据进行整理、描述和分析.下面给出了部分信息.
a.七年级学生知识竞赛成绩的平均数、中位数、众数、优秀率(80分及以上)如下表所示:
年级 | 平均数 | 中位数 | 众数 | 优秀率 |
七年级 | 84. 2 | 77 | 74 | 45﹪ |
b.八年级学生知识竞赛成绩的扇形统计图如下(数据分为5组,A:50≤x≤59; B:60≤x≤69;C:70≤x≤79;D:80≤x≤89;E:90≤x≤100)
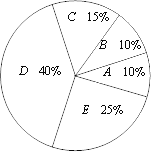
c.八年级学生知识竞赛成绩在D组的是:87 88 88 88 89 89 89 89
根据以上信息,回答下列问题:
(1)八年级学生知识竞赛成绩的中位数是 分;
(2)请你估计该校七、八年级所有学生中达到“优秀”的有多少人?
(3)下列结论:①八年级成绩的众数是89分;②八年级成绩的平均数可能为86分;③八年级成绩的极差可能为50分.其中所有正确结论的序号是 .