题目内容
【题目】在△ABC中，∠AOB=90°，AO=BO，直线MN经过点O，且AC⊥MN于C，BD⊥MN于D
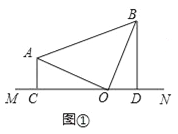
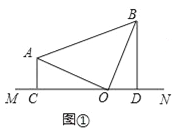
（1）当直线MN绕点O旋转到图①的位置时，求证：CD=AC+BD；
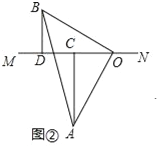
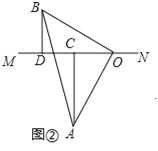
（2）当直线MN绕点O旋转到图②的位置时，求证：CD=AC﹣BD；
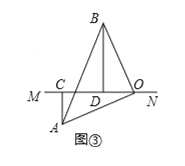
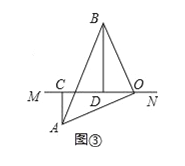
（3）当直线MN绕点O旋转到图③的位置时，试问：CD、AC、BD有怎样的等量关系？请写出这个等量关系，并加以证明．
【答案】（1）证明见解析；（2）证明见解析；（3）CD=BD﹣AC，证明见解析．
【解析】试题分析：（1）通过证明△ACO≌△ODB得到OC=BD，AC=OD，则CD=AC+BD；
（2）通过证明△ACO≌△ODB得到OC=BD，AC=OD，则CD=AC-BD；
（3）通过证明△ACO≌△ODB得到OC=BD，AC=OD，则CD=BD-AC．
试题解析：（1）如图1，
∵△AOB中，∠AOB=90°，
∴∠AOC+∠BOD=90°，
直线MN经过点O，且AC⊥MN于C，BD⊥MN于D，
∴∠ACO=∠BDO=90°
∴∠AOC+∠OAC=90°，
∴∠OAC=∠BOD，
在△ACO和△ODB中，
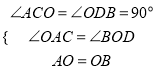
∴△ACO≌△ODB（AAS），
∴OC=BD，AC=OD，
∴CD=AC+BD；
（2）如图2，
∵△AOB中，∠AOB=90°，
∴∠AOC+∠BOD=90°，
直线MN经过点O，且AC⊥MN于C，BD⊥MN于D，
∴∠ACO=∠BDO=90°
∴∠AOC+∠OAC=90°，
∴∠OAC=∠BOD，
在△ACO和△ODB中，
,
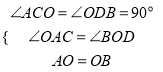∴△ACO≌△ODB（AAS），
∴OC=BD，AC=OD，
∴CD=OD﹣OC=AC﹣BD，即CD=AC﹣BD．
（3）如图3，
∵△AOB中，∠AOB=90°，
∴∠AOC+∠BOD=90°，
直线MN经过点O，且AC⊥MN于C，BD⊥MN于D，
∴∠ACO=∠BDO=90°
∴∠AOC+∠OAC=90°，
∴∠OAC=∠BOD，
在△ACO和△ODB中，
,
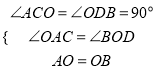∴△ACO≌△ODB（AAS），
∴OC=BD，AC=OD，
∴CD=OC﹣OD=BD﹣AC，
即CD=BD﹣AC．
