题目内容
【题目】如图,在△ABC中,AB=AC,点D是BC边上的中点,连接AD.
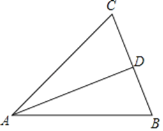
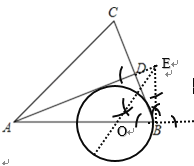
(1)在AB边上求作一点O,使得以O为圆心,OB长为半径的圆与AD相切;(不写作法,保留作图痕迹)
(2)设⊙O与AD相切于点M,已知BD=8,DM=4,求⊙O的半径.
【答案】(1)见解析;(2)5
【解析】
(1)过点B作AB的垂线与AD的延长线交于点E,作∠AEB的平分线交AB于点O,以O为圆心OB为半径作⊙O即可;
(2)根据切线的性质构造矩形和直角三角形根据勾股定理即可求解.
(1)如图即为所求作的图形.
(2)连接OM、作ON⊥BD于点N,
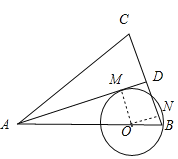
∵AB=AC,点D是BC边上的中点,
∴AD⊥BC,
∵⊙O与AD相切于点M,
∴OM⊥AD,
∴OMDN是矩形,
在Rt△OBN ,设⊙O半径为r,则DN=r,BN=8﹣r,ON=DM=4,
根据勾股定理,得
(8﹣r)2+16=r2
解得r=5.
答:⊙O的半径为5.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目