题目内容
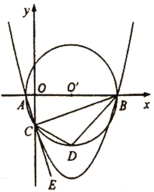
【题目】如图,点A是抛物线![]() 对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为______________.
对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为______________.
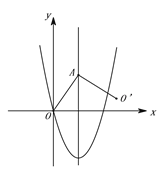
【答案】(2,2)或(2,-1)
【解析】
∵抛物线y=x2-4x对称轴为直线x=-![]()
∴设点A坐标为(2,m),
如图所示,作AP⊥y轴于点P,作O′Q⊥直线x=2,
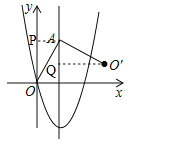
∴∠APO=∠AQO′=90°,
∴∠QAO′+∠AO′Q=90°,
∵∠QAO′+∠OAQ=90°,
∴∠AO′Q=∠OAQ,
又∠OAQ=∠AOP,
∴∠AO′Q=∠AOP,
在△AOP和△AO′Q中,
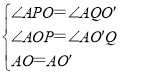
∴△AOP≌△AO′Q(AAS),
∴AP=AQ=2,PO=QO′=m,
则点O′坐标为(2+m,m-2),
代入y=x2-4x得:m-2=(2+m)2-4(2+m),
解得:m=-1或m=2,
∴点A坐标为(2,-1)或(2,2),
故答案是:(2,-1)或(2,2).

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目