题目内容
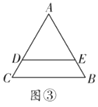
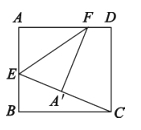
【题目】两个全等的等腰直角三角形,斜边长为2,按如图放置,其中一个三角形45°角的项点与另一个三角形的直角顶点A重合,若三角形ABC固定,当另一个三角形绕点A旋转时,它的角边和斜边所在的直线分别与边BC交于点E、F,设BF=![]() CE=
CE=![]() 则
则![]() 关于
关于![]() 的函数图象大致是( )
的函数图象大致是( )
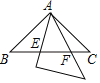
A.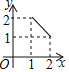 B.
B.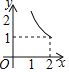 C.
C.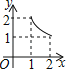 D.
D.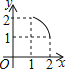
【答案】C
【解析】
由题意得∠B=∠C=45°,∠G=∠EAF=45°,推出△ACE∽△ABF,得到∠AEC=∠BAF,根据相似三角形的性质得到![]() ,于是得到结论.
,于是得到结论.
解:如图:
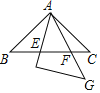
由题意得∠B=∠C=45°,∠G=∠EAF=45°,
∵∠AFE=∠C+∠CAF=45°+∠CAF,∠CAE=45°+∠CAF,
∴∠AFB=∠CAE,
∴△ACE∽△ABF,
∴∠AEC=∠BAF,
∴△ABF∽△CAE,
∴![]() ,
,
又∵△ABC是等腰直角三角形,且BC=2,
∴AB=AC=![]() ,又BF=x,CE=y,
,又BF=x,CE=y,
∴![]() ,
,
即xy=2,(1<x<2).
故选:C.

练习册系列答案
相关题目
【题目】问题:探究函数y=x+![]() 的图象和性质.
的图象和性质.
小华根据学习函数的方法和经验,进行了如下探究,下面是小华的探究过程,请补充完整:
(1)函数的自变量x的取值范围是:____;
(2)如表是y与x的几组对应值,请将表格补充完整:
x | … | ﹣3 | ﹣2 | ﹣ | ﹣1 |
|
| 1 |
| 2 | 3 | … |
y | … | ﹣3 | ﹣3 |
| ﹣3 | ﹣4 | 4 |
| 3 | … |
(3)如图,在平面直角坐标系中描点并画出此函数的图象;
(4)进一步探究:结合函数的图象,写出此函数的性质(一条即可).