题目内容
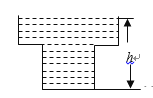
【题目】如图,点B在线段AF上,分别以AB、BF为边在线段AF的同侧作正方形ABCD和正方形BFGE,连接CF和DE,CF交EG于点H.
(1)若E是BC的中点,求证:DE=CF;
(2)若∠CDE=30°,求![]() 的值.
的值.

【答案】(1) DE=CF;(2)![]()
【解析】试题分析:(1)根据线段中点的定义可得BE=CE,再根据正方形的四条边都相等可得BC=CD,BE=BF,然后求出BF=CE,再利用“边角边”证明△BCF和△CDE全等,根据全等三角形对应边相等可得DE=CF;
(2)设CE=x,根据∠CDE的正切值表示出CD,然后求出BE,从而得到∠BCF的正切值,再根据两直线平行,内错角相等可得∠BCF=∠GFH,然后根据等角的正切值相等解答即可.
试题解析:(1)证明:∵E是BC的中点,
∴BE=CE,
在正方形ABCD和正方形BFGE中,BC=CD,BE=BF,
∴BF=CE,
在△BCF和△CDE中,
 ,
,
∴△BCF≌△CDE(SAS),
∴DE=CF;
(2)设CE=x,∵∠CDE=30°,
∴tan∠CDE=![]() ,
,
∴CD= ![]() ,
,
∵正方形ABCD的边BC=CD,
∴BE=BC﹣CE= ![]() ﹣x,
﹣x,
∵正方形BFGE的边长BF=BE,
∴tan∠BCF=![]() ,
,
∵正方形BGFE对边BC∥GF,
∴∠BCF=∠GFH,
∵tan∠GFH=![]() ,
,
∴![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目