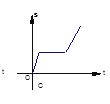��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��x�ᣬy��ֱ��ڵ�A(��4��0)��B(0��3)������P�ӵ�O��������x�Ḻ������ÿ��1����λ���ٶ��˶���ͬʱ����Q�ӵ�B������������BO������ÿ��2����λ���ٶ��˶�������P��PC��AB�ڵ�C������PQ��CQ����PQ��CQΪ�ڱ߹���ƽ���ı���PQCD�����P�˶���ʱ��Ϊt�룮
(1)����Q���߶�OB��ʱ���ú�t�Ĵ���ʽ��ʾPC��AC�ij���
(2)���˶������У�
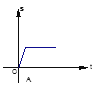
�ٵ���D����x����ʱ���������������t��ֵ��
������D������ABO�ڲ�(�������߽�)ʱ��ֱ��д��t��ȡֵ��Χ��
(3)����Q����x��ĶԳƵ�Q��������CQ�������˶������У��Ƿ����ijʱ��ʹ��A��P��C�����Բ����CQQ�������е�һ�������У������ڣ������t��ֵ���������ڣ���˵�����ɣ�



���𰸡���1��PC��![]() (4��t)��AC��
(4��t)��AC��![]() (4��t)����2����
(4��t)����2����![]() ����
����![]() ����3�����ڣ�
����3�����ڣ�![]() ��
��![]()
�������������������1���������AB����Rt��ACP��PA=4-t������sin��OAB=![]() �����PC������cos��OAB=
�����PC������cos��OAB=![]() �����AC��
�����AC��
��2�����ٵ�D��x����ʱ����QC��OA����![]() ���ɴ˼��ɽ�����⣮
���ɴ˼��ɽ�����⣮
�ڵ���D��AB��ʱ����PQ��AB����![]() �����ʱ��t������٢���������ʱ�ġ�POQ��������ɽ�����⣮
�����ʱ��t������٢���������ʱ�ġ�POQ��������ɽ�����⣮
��3����QC���M����ʱ����QC��CM������֤��QB=QC����QN��BC��N������cos��ABO=![]() ���г����̼��ɽ�����⣬��CQ���ǡ�M����ʱ���������ƣ�
���г����̼��ɽ�����⣬��CQ���ǡ�M����ʱ���������ƣ�
���������(1)��ͼ1�У�

��OA��8��OB��6����AB��![]() ��5��
��5��
��Rt��ACP��PA��4��t��

��sin��OAB��![]() ����PC��
����PC��![]() (4��t)��
(4��t)��
��cos��OAB��![]() ����AC��
����AC��![]() (4��t)��
(4��t)��
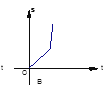
(2)�ٵ�D��x����ʱ����ͼ2�У�
��QC��OA����![]() ��
��![]() ��
��
���![]() ��
��
��![]() ʱ����D��x���ϣ�
ʱ����D��x���ϣ�
��![]() ��
��
(3)��ͼ3�У�

��Q(0��3��2t)��Q��(0��2t��3)��
��QC���M����ʱ����QC��CM��
���QCM��90�㣬���QCP+��PCM��90�㣬�ߡ�QCP+��QCB��90�㣬
���BCQ����PCM����CPM��
�ߡ�CPM+��PAC��90�㣬��OBA+��OAB��90�㣬
���APC����OBA�����QBC����QCB��
��BQ��CQ����QN��BC��N��
��cos��ABO��![]() ����
����![]() ��
��
���![]() ��
��
��CQ���ǡ�M����ʱ��ͬ���ɵ�![]() �����
�����![]() ��
��
��![]() ��
��![]() ʱ����A��P��C�����Բ����CQQ�������е�һ�������У�
ʱ����A��P��C�����Բ����CQQ�������е�һ�������У�