题目内容
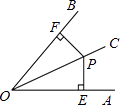
【题目】如图甲,直线PA交O于A、E两点,PA的垂线CD切O于点C,过点A作O的直径AB.
(1)求证:AC平分∠DAB;
(2)将直线CD向下平行移动,在将直线CD向下平行移动的过程中,如图乙、丙,试指出与∠DAC相等的角(不要求证明).
(3)在图甲中,若DC+DA=6,O的直径为10,求AE的长度.
【答案】
(1)
证明:如图1,连接OC,
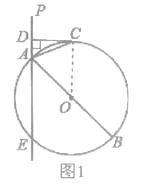
∵OA、OC是O的半径,
∴ OA=OC.
∴ ∠OAC=∠OCA,
∵CD切于圆O于点C,
∴ CD⊥OC,
又∵CD⊥PA,
∴ OC//PA,
∴ ∠PAC=∠OCA,
∴ ∠OAC=∠PAC,
∴ AC平分∠DAB.
(2)
∠DAC=∠BAF,理由如下:
如图2,连接BC,
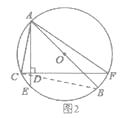
∵AB是圆O的直径,
∴∠ACB=90°,
∴∠ACF+∠BCF=90°,
又∵在Rt△ACD中,∠DAC+∠ACD=90°,
∴∠DAC=∠FCB,
又∵∠BAF =∠FCB,
∴∠DAC=∠BAF.
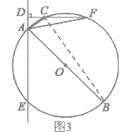
如图3,∵AB是圆O的直径,
∴∠ACB=90°,
∴∠CAB+∠CBA=90°,
又∵∠DAF+∠AFD=90°,∠AFD =∠CBA,
∴∠DAF=∠CAB,
∴∠DAF-∠CAF=∠CAB-∠CAF.
∴∠DAC=∠BAF.
(3)
解:如图4所示:连接OC,过点A作AF⊥CO,垂足为F,连接CB、CE.
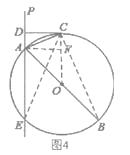
∵DC垂直AE,OC垂直DC,AF垂直CO,
∴ 四边形AFCD为矩形.
∴ DC=AF,AD=CF.
设AD的长为x,则AF=6-x,OF=5-x.
在Rt△AFO中,OA2=AF2+OF2,即:25=(6-x)2+(5-x)2,
解得:x1=2,x2=9(舍去).
∴ AD=2,DC=4.
由(1)可知:∠DAC=∠BAC,
又∵∠CAD+∠DCA=90°,∠CAB+∠ABC=90°,
∴ ∠DCA=∠ABC,
∵∠DEC=∠ABC,
∴ ∠DEC=∠DCA,
又∵∠EDC=∠ADC,
∴ △EDC~△CDA,
∴ ![]() ,即:
,即: ![]() ,
,
∴ DE=8,
∴ AE=DE-AD=8-2=6.
【解析】(1)需要证明∠OAC=∠PAC,连接OC,则OC=OA,则∠OAC=∠OCA,所以需要证明∠PAC=∠OCA,则需要证明AD//OC,而CD⊥PA,则CD⊥OC,由CD切于圆O于点C,可证得;(2)如图2,根据两角和为90°,等量代换得到∠DAC=∠FCB,由同弧所对的圆周角相等可得∠BAF =∠FCB,从而证得∠DAC=∠BAF;如图3,同理由两角和为90°,等量代换得到∠DAF=∠CAB,则∠DAC=∠BAF.(3)连接OC,过点A作AF⊥CO,垂足为F,连接CB、CE,则易得DC=AF,AD=CF,可设AD的长为x,则AF=6-x,OF=5-x,在Rt△AFO中,由勾股定理构造方程解出x,由(1)和(2)可证得∠DEC=∠DCA,又∠EDC=∠ADC,则△EDC~△CDA,由对应边成比例解出DE,则AE=DE-AD.
【考点精析】认真审题,首先需要了解圆的定义(平面上到定点的距离等于定长的所有点组成的图形叫做圆.定点称为圆心,定长称为半径),还要掌握切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径)的相关知识才是答题的关键.