题目内容
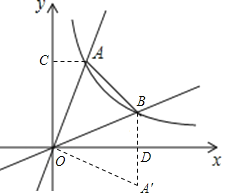
【题目】如图,在平面直角坐标系中,反比例函数![]() 与正比例函数
与正比例函数![]() 的图像分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.
的图像分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.

【答案】3
【解析】
根据AB两点分别在反比例函数和正比例函数图象上,且存在相同k值,可先证明点A横坐标和B纵坐标相等,利用旋转知识证明△AOB面积为△A′OB的面积,再利用反比例函数k的几何意义.
如图,过B作BD⊥x轴于点D,过A作AC⊥y轴于点C.
设点A横坐标为a,则A![]() ,
,
∵A在正比例函数y=kx图象上
∴![]() ,
,
∴![]() ,
,
同理,设点B横坐标为b,则B![]()
∴![]() ,
,
∴k=![]() ,
,
∴![]() ,
,
∴ab=3,
当点A坐标为![]() 时,点B坐标为
时,点B坐标为![]()
∴OC=OD,
将△AOC绕点O顺时针旋转90°,得到△ODA′,
∵BD⊥x轴,
∴B、D、A′共线,
∵∠AOB=45°,∠AOA′=90°,
∴∠BOA′=45°,
∵OA=OA′,OB=OB,
∴△AOB≌△A′OB,
∵S△BOD=S△AOC=3×![]() =
=![]() ,
,
∴S△AOB=3;
故答案为:3

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
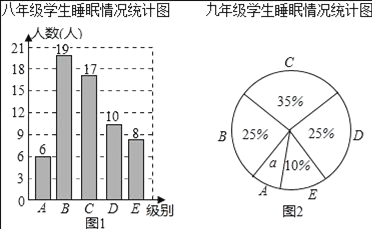
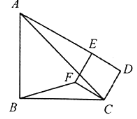
【题目】为了解某校八、九年级部分学生的睡眠情况,随机抽取了该校八、九年级部分学生进行调查,已知抽取的八年级与九年级的学生人数相同,利用抽样所得的数据绘制如图的统计图表:
睡眠情况分段情况如下
组别 | 睡眠时间x(小时) |
|
|
|
|
|
|
|
|
|
|
根据图表提供的信息,回答下列问题:
(Ⅰ)直接写出统计图中![]() 的值 ;
的值 ;
(Ⅱ)睡眠时间少于6.5小时为严重睡眠不足,则从该校八、九年级各随机抽一名学生,被抽到的这两位学生睡眠严重不足的可能性分别有多大?