题目内容
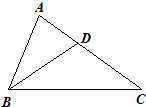 21、如图,点D在AC上,且∠ABD=∠C,AB=4,CD=6,求AD的长.
21、如图,点D在AC上,且∠ABD=∠C,AB=4,CD=6,求AD的长.分析:由已知先证△ABC∽△ADB,再根据相似三角形的性质,相似三角形的对应边成比例,即可求出AD的值.
解答:解:∵∠ABD=∠C,∠A=∠A
∴△ABD∽△ACB.
∴AB2=AD•AC
设AD=x,得x(x+6)=16
解得:x1=2或x2=-8(舍去)
∴AD=2.
∴△ABD∽△ACB.
∴AB2=AD•AC
设AD=x,得x(x+6)=16
解得:x1=2或x2=-8(舍去)
∴AD=2.
点评:本题考查相似三角形的判定和性质.识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角,可利用数形结合思想根据图形提供的数据计算对应角的度数、对应边的值.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
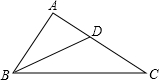 如图,点D在AC上,且∠ABD=∠C,AB=CD=2,则AD=
如图,点D在AC上,且∠ABD=∠C,AB=CD=2,则AD=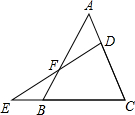 如图,点D在AC上,点E在CB的延长线上,且BE=AD,ED交AB于点F,求证:EF•BC=AC•FD.
如图,点D在AC上,点E在CB的延长线上,且BE=AD,ED交AB于点F,求证:EF•BC=AC•FD. 已知:如图,点O在AC上,⊙O过B,C两点,交AC于点D,AB与⊙O相切.
已知:如图,点O在AC上,⊙O过B,C两点,交AC于点D,AB与⊙O相切.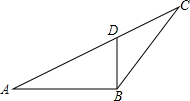 如图,点D在AC上,∠BAD=∠DBC.
如图,点D在AC上,∠BAD=∠DBC.