��Ŀ����
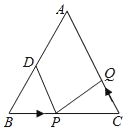
����Ŀ����ͼ��ʾ���ڡ�ABC�У�AB��AC��20cm��BC��16cm��DΪAB�е㣬�����P���߶�BC���ɵ�B�������C�˶���ͬʱ��Q���߶�CA���ɵ�C�������A�˶������˶�ʱ��Ϊt��s����
��1������P���Q���ٶȶ���2cm/s���ʾ�������ʱ���BPD���CQPȫ�ȣ�˵�����ɣ�
��2������P���ٶȱȵ�Q���ٶȶ���2cm/s��������ʱ���BPD���CQPȫ�ȣ��������ʱ������ٶȣ�
��3������P����Q�ֱ��ԣ�2�����ٶ�ͬʱ��B��C����������ʱ���ء�ABC�����˶����ʾ�������ʱ���P���Q��һ���������������ڡ�ABC���������ϣ���������������B�ľ��룮

���𰸡���1������3s��BPD���CQPȫ�ȣ���2�����˶�ʱ��Ϊ1sʱ����BPD���CPQȫ�ȣ���ʱ��P���ٶ�Ϊ8cm/s����Q���ٶ�Ϊ10cm/s����3����һ��������AB���ϣ���ʱ���������B�ľ���8cm��
��������
��1�����ݵ��������ε����ʿɵó���B����C���ɵ�P��Qͬ��ͬʱ�����ɵó�BP��CQ�����ȫ�������ε��ж������ɵó���BD��CPʱ��BPD���CQPȫ�ȣ��������ɵó�����t��һԪһ�η��̣���֮���ɵó����ۣ�
��2�����P���ٶ�Ϊxcm/s�����Q���ٶ�Ϊ��x+2��cm/s����BP��CQ����B����C���ȫ�������ε����ʿɵó�BD��CQ��BP��CP��8���������ɵó�����t��x�ķ����飬��֮���ɵó����ۣ�
��3������·�̣��ٶȡ�ʱ���ϵ�P��Q���������ɵó�����t��һԪһ�η��̣���֮�����tֵ���ɵ�Q��·�̣���Q���ٶȡ��˶�ʱ��������Q��·�̣��ٽ��CA��AB��BC�ij��ȣ������ҳ���P��Q��һ������ʱ��λ�ã�����ý⣮
�⣺��1����AB��AC��
���B����C��
�ߵ�P���Q���ٶȶ���2cm/s��
��BP��CQ��
�൱BD��CPʱ����BPD���CQPȫ�ȣ���10��16��2t��
���t��3��
�ྭ��3s��BPD���CQPȫ�ȣ�
��2�����P���ٶ�Ϊxcm/s�����Q���ٶ�Ϊ��x+2��cm/s��
��BP��CQ����B����C��
��BD��CQ��BP��CP��8��
��![]() ��
��
��ã�![]() ��
��
�൱�˶�ʱ��Ϊ1sʱ����BPD���CPQȫ�ȣ���ʱ��P���ٶ�Ϊ8cm/s����Q���ٶ�Ϊ10cm/s��
��3����������ã�10t��40+8t��
��ã�t��20��
��Q��·�̣�10��20��200��cm����
��200����20+20+16����3+20+12��20��12��8��
���һ��������AB���ϣ���ʱ���������B�ľ���8cm��