Question

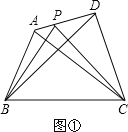
【题目】提出问题：如图①，在四边形ABCD中，P是AD边上任意一点，

△PBC与△ABC和△DBC的面积之间有什么关系？

探究发现：为了解决这个问题，我们可以先从一些简单的、特殊的情形入手：

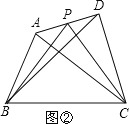
（1）当AP=AD时（如图②）：

∵AP=AD，△ABP和△ABD的高相等，

∴S△ABP=S△ABD．

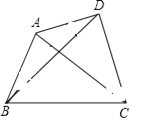
∵PD=AD﹣AP=AD，△CDP和△CDA的高相等，

∴S△CDP=S△CDA．

∴S△PBC=S四边形ABCD﹣S△ABP﹣S△CDP

=S四边形ABCD﹣S△ABD﹣S△CDA

=S四边形ABCD﹣（S四边形ABCD﹣S△DBC）﹣（S四边形ABCD﹣S△ABC）

=S△DBC+S△ABC．

（2）当AP=AD时，探求S△PBC与S△ABC和S△DBC之间的关系，写出求解过程；

（3）当AP=AD时，S△PBC与S△ABC和S△DBC之间的关系式为：　 　；

（4）一般地，当AP=AD（n表示正整数）时，探求S△PBC与S△ABC和S△DBC之间的关系，写出求解过程；

问题解决：当AP=AD（0≤≤1）时，S△PBC与S△ABC和S△DBC之间的关系式为：　 　．

Answer 1

【答案】答案见解析

【解析】试题分析：（2）仿照（1）的方法，只需把换为即可；
（3）注意由（1）（2）得到一定的规律；
（4）综合（1）（2）（3）得到面积和线段比值之间的一般关系；
（5）利用（4），得到更普遍的规律．

试题解析：(2)∵△ABP和△ABD的高相等，

又 △CDP和△CDA的高相等，

∴S△PBC=S四边形ABCDS△ABPS△CDP=S四边形ABCDS△ABDS△CDA，

=S四边形ABCD (S四边形ABCDS△DBC) (S四边形ABCDS△ABC)，

(3)

(4)

△ABP和△ABD的高相等，

又△CDP和△CDA的高相等，

∴S△PBC=S四边形ABCDS△ABPS△CDP=S四边形ABCDS△ABDS△CDA，

=S四边形ABCD (S四边形ABCDS△DBC) (S四边形ABCDS△ABC)，

问题解决：