题目内容
【题目】如图，直线y=﹣2x+4交y轴于点A，交抛物线
于点B（3，﹣2），抛物线经过点C（﹣1，0），交y轴于点D，点P是抛物线上的动点，作PE⊥DB交DB所在直线于点E．
（1）求抛物线的解析式；
（2）当△PDE为等腰直角三角形时，求出PE的长及P点坐标；
（3）在（2）的条件下，连接PB，将△PBE沿直线AB翻折，直接写出翻折点后E的对称点坐标．
【答案】（1）
；（2）PE=5或2，P（2，﹣3）或（5，3）；（3）E的对称点坐标为（
，﹣
）或（3.6，﹣1.2）．
【解析】试题分析：（1）把B（3，﹣2），C（﹣1，0）代入
即可得到结论；
（2）由
求得D（0，﹣2），根据等腰直角三角形的性质得到DE=PE，列方程即可得到结论；
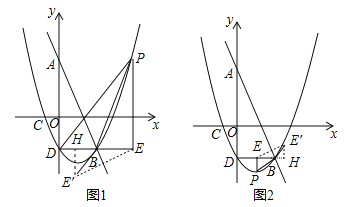
（3）①当P点在直线BD的上方时，如图1，设点E关于直线AB的对称点为E′，过E′作E′H⊥DE于H，求得直线EE′的解析式为
，设E′（m， 
），根据勾股定理即可得到结论；②当P点在直线BD的下方时，如图2，设点E关于直线AB的对称点为E′，过E′作E′H⊥DE于H，得到直线EE′的解析式为
，设E′（m， 
），根据勾股定理即可得到结论．
试题解析：解：（1）把B（3，﹣2），C（﹣1，0）代入
得： 
，∴
，∴抛物线的解析式为
；
（2）设P（m， 
），在
中，当x=0时，y=﹣2，∴D（0，﹣2），∵B（3，﹣2），∴BD∥x轴，∵PE⊥BD，∴E（m，﹣2），∴DE=m，PE=
，或PE=
，∵△PDE为等腰直角三角形，且∠PED=90°，∴DE=PE，∴m= 
，或m= 
，解得：m=5，m=2，m=0（不合题意，舍去），∴PE=5或2，P（2，﹣3）或（5，3）；
（3）①当P点在直线BD的上方时，如图1，设点E关于直线AB的对称点为E′，过E′作E′H⊥DE于H，由（2）知，此时，E（5，﹣2），∴DE=5，∴BE′=BE=2，∵EE′⊥AB，∴设直线EE′的解析式为
，∴﹣2=
×5+b，∴b=﹣
，∴直线EE′的解析式为
，设E′（m， 
），∴E′H=﹣2﹣
= 
，BH=3﹣m，∵E′H2+BH2=BE′2，∴（
）2+（3﹣m）2=4，∴m=
，m=5（舍去），∴E′（
，﹣
）；
②当P点在直线BD的下方时，如图2，设点E关于直线AB的对称点为E′，过E′作E′H⊥DE于H，由（2）知，此时，E（2，﹣2），∴DE=2，∴BE′=BE=1，∵EE′⊥AB，∴设直线EE′的解析式为
，∴﹣2=
×2+b，∴b=﹣3，∴直线EE′的解析式为
，设E′（m， 
），∴E′H=
=
，BH=m﹣3，∵E′H2+BH2=BE′2，∴（
）2+（m﹣3）2=1，∴m=3.6，m=2（舍去），∴E′（3.6，﹣1.2）．
综上所述，E的对称点坐标为（
，﹣
）或（3.6，﹣1.2）．
