题目内容
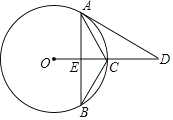
【题目】已知在△ABC中,∠ABC=90°,AB=9,BC=12.点Q是线段AC上的一个动点,过点Q作AC的垂线交射线AB于点P.当△PQB为等腰三角形时,则AP的长为_______.
【答案】5或18
【解析】
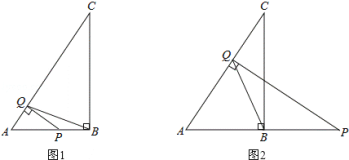
当△PQB为等腰三角形时,有两种情况: ①当点P在线段AB上时,如题图1所示.由△AQP∽△ABC即可计算AP的长;②当点P在线段AB的延长线上时,如题图2所示,利用角之间的关系,证明点B为线段AP的中点,从而可以求出AP.
∵∠A+∠APQ=90°,∠A+∠C=90°,
∴∠APQ=∠C.
∵∠A=∠A,
∴△APQ∽△ACB.
在Rt△ABC中,AB=9,BC=12,由勾股定理得:AC=15,
①当点P在线段AB上时,如题图1所示,
∵∠BPQ为钝角,
∴当△PQB为等腰三角形时,只可能是PB=PQ.
∵△APQ∽△ACB,
∴![]() ,即
,即![]() ,解得:PB=4,
,解得:PB=4,
∴AP=AB﹣PB=9-4=5;
②当点P在线段AB的延长线上时,如题图2所示,
∵∠QBP为钝角,
∴当△PQB为等腰三角形时,只可能是BP=BQ,
∴∠BQP=∠P,
∵∠BQP+∠AQB=90°,∠A+∠P=90°,
∴∠AQB=∠A,
∴BQ=AB,
∴AB=BP,点B为线段AB中点,
∴AP=2AB=2×9=18.
综上所述,当△PQB为等腰三角形时,AP的长为5或18.
故答案是:5或18.

【题目】如图,在![]() 中
中![]() ,
,![]() ,
,![]() 点P从点B出发,沿折线
点P从点B出发,沿折线![]() 运动,当它到达点A时停止,设点P运动的路程为
运动,当它到达点A时停止,设点P运动的路程为![]() 点Q是射线CA上一点,
点Q是射线CA上一点,![]() ,连接
,连接![]() 设
设![]() ,
,![]() .
.
![]() 求出
求出![]() ,
,![]() 与x的函数关系式,并注明x的取值范围;
与x的函数关系式,并注明x的取值范围;
![]() 补全表格中
补全表格中![]() 的值;
的值;
x | 1 | 2 | 3 | 4 | 6 |
| ______ | ______ | ______ | ______ | ______ |
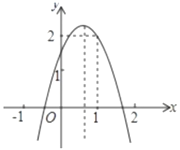
以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点,并在x的取值范围内画出![]() 的函数图象:
的函数图象:
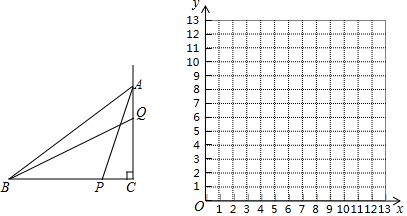
![]() 在直角坐标系内直接画出
在直角坐标系内直接画出![]() 函数图象,结合
函数图象,结合![]() 和
和![]() 的函数图象,求出当
的函数图象,求出当![]() 时,x的取值范围.
时,x的取值范围.
【题目】今年5月12日是“母亲节”,某校开展“感恩母亲,做点家务”活动为了了解同学们在母亲节这一天做家务情况,学校随机抽查了部分同学,并用得到的数据制成如下不完整的统计表:
做家务时间(小时) | 人数 | 所占百分比 |
| 15 | 30% |
| 31 | 62% |
|
| 4% |
| 2 |
|
合计 |
| 100% |
(1)统计表中的![]() __________,
__________,![]() __________;
__________;
(2)小君计算被抽查同学做家务时间的平均数是这样的:
第一步:计算平均数的公式是![]() ,
,
第二步:该问题中![]() ,
,![]()
![]() ,
,![]() ,
,![]() ;
;
第三步:![]() (小时)
(小时)
小君计算的过程正确吗?如果不正确,请你计算出正确的做家务时间的平均数;
(3)现从![]() ,
,![]() 两组中任选2人,求这2人都在
两组中任选2人,求这2人都在![]() 组中的概率(用树形图法或列表法).
组中的概率(用树形图法或列表法).