题目内容
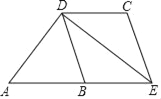
【题目】如图,已知在△ADE中,∠ADE=90°,点B是AE的中点,过点D作DC∥AE,DC=AB,连结BD、CE.
(1)求证:四边形BDCE是菱形;
(2)若AD=8,BD=6,求菱形BDCE的面积.
【答案】(1)证明见解析;(2)S菱形BDCE=16![]() .
.
【解析】
(1)证明菱形先证明四边形是平行四边形,再利用一组邻边相等证明菱形.(2)求菱形的两条对角线长度,再求菱形的面积.
(1)证明:在Rt△ADB中,∵∠ADB=90°,AB=BE,
∴DB=![]() AB=AB=BE,
AB=AB=BE,
∵DC∥BE,DC=AB=BE,
∴四边形BECD是平行四边形,
∵BD=BE,
∴四边形BECD是菱形.
(2)解:连接BC交DE于O.
∵四边形DBEC是菱形,
∴BC⊥DE,
∴BO∥AD,∵AB=BE,
∴DO=OE,
∴OB=![]() AD=4,OD==2
AD=4,OD==2![]() ,
,
∴BC=8,DE=4![]() ,
,
∴S菱形BDCE=![]() BCDE=16
BCDE=16![]() .
.

练习册系列答案
相关题目







