题目内容
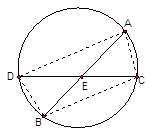
(本题8分)如图,AB为⊙O的直径,CD⊥AB于点E,交⊙O于点D,OF⊥AC于点F.
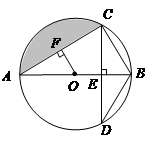
(1)请写出两条与BC有关的正确结论;
(2)当∠D=30°,BC=1时,求圆中阴影部分的面积.

(1)请写出两条与BC有关的正确结论;
(2)当∠D=30°,BC=1时,求圆中阴影部分的面积.
(1)答案不唯一,只要合理均可.例如:
(2)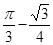 ①
①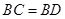 ;②
;②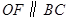 ;③
;③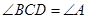 ;④
;④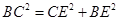 ;⑤
;⑤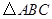 是直角三角形;⑥
是直角三角形;⑥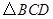 是等腰三角形.
是等腰三角形.
(2)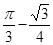
(2)
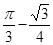 ①
①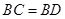 ;②
;②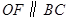 ;③
;③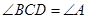 ;④
;④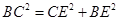 ;⑤
;⑤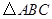 是直角三角形;⑥
是直角三角形;⑥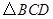 是等腰三角形.
是等腰三角形. (2)
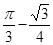
试题分析:(1)根据垂径定理可以进一步证明△CBE≌△DBE,得出BC=BD
根据直径所对的圆周角等于90°,可以得出BC⊥AC,进而得出OF∥BC
根据垂径定理可以得出弧BC和弧BD相等,所以∠BCD=∠A
根据CE⊥BE,根据勾股定理可以得出
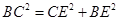
根据直径所对的圆周角等于90°,可以得出
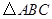 是直角三角形
是直角三角形根据垂径定理可以进一步证明△CBE≌△DBE,得出BC=BD,即
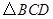 是等腰三角形
是等腰三角形(2)连接CO
∠D=30°,同弧所对圆周角相等,所以∠A=∠D,∴∠A=30°
因为AB是直径,所以∠ACB=90°
∴AB=2BC=2
在Rt△AFO中
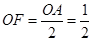 ,根据勾股定理得出,
,根据勾股定理得出,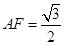 ,AC=2AF=
,AC=2AF=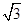
阴影部分面积= S扇形AOC-S△AOC
S△AOC =
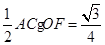
因为CO=AO,OF=OF,根据垂径定理,AF=CF
所以△AOF≌△COF,所以∠COF=∠AOF=60°,
所以∠AOC=120°
所以S扇形AOC =
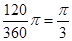
阴影部分面积=
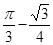
点评:难度较大,主要在掌握圆的综合运用,包括圆周角,垂径定理的运用,勾股定理的运用,主要把握阴影部分面积可以由几种特殊的图形加减变化而来。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
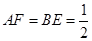 ,联结FC、ED,CD=2,AB=6。
,联结FC、ED,CD=2,AB=6。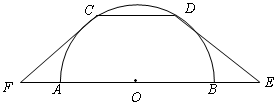
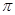 厘米的细铁丝剪成两段,并把每段铁丝围成圆,设所得两圆半径分别为r和R,面积分别为S1和S2.
厘米的细铁丝剪成两段,并把每段铁丝围成圆,设所得两圆半径分别为r和R,面积分别为S1和S2.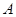 和圆
和圆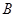 相切,两圆的圆心距为8cm,圆
相切,两圆的圆心距为8cm,圆