题目内容
【题目】若菱形的边长和一条对角线的长均为2 cm，则菱形的面积是( )
A. 4 
B. 
C. 
D. 3
【答案】C
【解析】
试题由四边形ABCD是菱形，可得菱形的四条边都相等AB=BC=CD=AD，菱形的对角线互相平分且相等即AC⊥BD，OA=OC，OB=OD，又因为菱形的边长和一条对角线的长均为2cm，易求得OB=1cm，则可得AC的值，根据菱形的面积等于积的一半，即可求得菱形的面积．
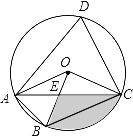
解：根据题意画出图形，如图所示：
∵四边形ABCD是菱形，
∴AB=BC=CD=AD=2cm，AC⊥BD，OA=OC，OB=OD，
又∵菱形的边长和一条对角线的长均为2cm，
∴AB=AD=BD=2cm，
∴OB=1cm，
∴OA=
cm，
∴AC=2cm，
∴菱形的面积为
cm2．
故选C．
练习册系列答案
相关题目
【题目】一家公司准备招聘一名英文翻译，对甲、乙和丙三名应试者进行了听、说、读、写 的英语水平测试，他们各项的成绩（百分制）如下：
应试者 | 听 | 说 | 读 | 写 |
甲 | 82 | 86 | 78 | 75 |
乙 | 73 | 80 | 85 | 82 |
丙 | 81 | 82 | 80 | 79 |
（1）如果这家公司按照这三名应试者的平均成绩（百分制）计算，从他们的成绩看，应该录取谁？
（2）如果这家公司想招一名口语能力较强的翻译，听、说、读、写成绩按照 3∶4∶2∶1 的权重确定，计算三名应试者的平均成绩（百分制），从他们的成绩看， 应该录取谁？
（3）如果这家公司想招一名笔译能力较强的翻译，听、说、读、写成绩按照 1∶2∶3∶4 的权重确定，计算三名应试者的平均成绩（百分制）．从他们的成绩看， 应该录取谁？
