题目内容
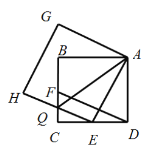
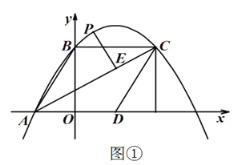
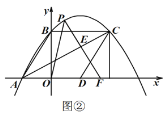
【题目】如图，将边长为8cm的正方形ABCD沿其对角线AC剪开，再把△ABC沿着AD方向平移，得到△A’B’C’，当两个三角形重叠部分的面积占△ACD面积的一半时，△ABC平移的距离是______．
【答案】4cm．
【解析】
根据平移的性质，结合阴影部分是平行四边形，△AA′H与△HCB′都是等腰直角三角形，则若设AA′=x，则阴影部分的底长为x，高A′D=8
x，根据平行四边形的面积公式即可列出方程求解．
解：设AC交A′B′于H，
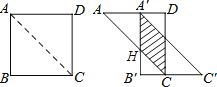
∵∠A=45°，∠D=90°
∴△A′HA是等腰直角三角形，
设A′H=AA′=x，则阴影部分的底长为x，高A′D=8x，
∵
，
∴
，
∴x（8-x）=16，
解得：x=4，
即AA′=4cm，
∴△ABC平移的距离是4cm；
故答案为：4cm．
【题目】参照学习函数的过程与方法，探究函数y=
的图象与性质．
因为y=
，即y=﹣
+1，所以我们对比函数y=﹣来探究．
列表：
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | ﹣ |
| 1 | 2 | 3 | 4 | … |
y=﹣ | … |
|
| 1 | 2 | 4 | ﹣4 | ﹣1 | 1 | ﹣ | ﹣ | … |
y= | … |
|
| 2 | 3 | 5 | ﹣3 | ﹣1 | 0 |
|
| … |
描点：在平面直角坐标系中，以自变量x的取值为横坐标，以y=
相应的函数值为纵坐标，描出相应的点，如图所示：
（1）请把y轴左边各点和右边各点，分别用一条光滑曲线顺次连接起来；
（2）观察图象并分析表格，回答下列问题：
①当x＜0时，y随x的增大而 ；（填“增大”或“减小”）
②y=的图象是由y=﹣的图象向 平移 个单位而得到；
③图象关于点 中心对称．（填点的坐标）
（3）设A（x1，y1），B（x2，y2）是函数y=的图象上的两点，且x1+x2=0，试求y1+y2+3的值．
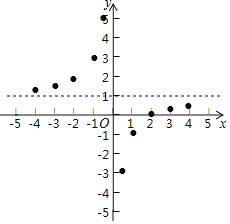
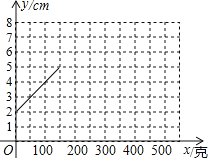
【题目】弹簧是一种利用弹性来工作的机械零件，用弹性材料制成的零件在外力作用下发生形变，除去外力后又恢复原状．某班同学在探究弹簧的长度与所受外力的变化关系时，通过实验记录得到的数据如下表：
砝码的质量x（克） | 0 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
指针的位置y（cm） | 2 | 3 | 4 | 5 | 6 | 7 | 7.5 | 7.5 | 7.5 |
小腾根据学习函数的经验，利用上述表格所反映出的y与x之间的变化规律，对该函数的图象与性质进行了探究，下面是小腾的探究过程，请补充完整．
（1）根据上述表格在平面直角坐标系中补全该函数的图象；
（2）根据画出的函数图象，写出：
①当x＝0时，y＝ ，它的实际意义是 ；
②当指针的位置y不变时，砝码的质量x的取值范围为 ．
