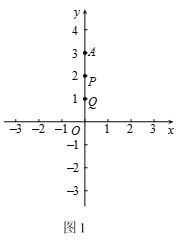题目内容
【题目】如图①,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,将
两点,将![]() 沿
沿![]() 轴正方向平移后,点
轴正方向平移后,点![]() 、点
、点![]() 的对应点分别为点
的对应点分别为点![]() 、点
、点![]() ,且四边形
,且四边形![]() 为菱形,连接
为菱形,连接![]() ,抛物线
,抛物线![]() 经过
经过![]() 三点,点
三点,点![]() 为
为![]() 上方抛物线上一动点,作
上方抛物线上一动点,作![]() ,垂足为
,垂足为![]()
![]() 求此抛物线的函数关系式;
求此抛物线的函数关系式;
![]() 求线段
求线段![]() 长度的最大值;
长度的最大值;
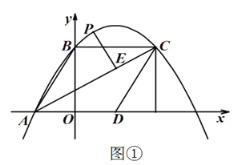
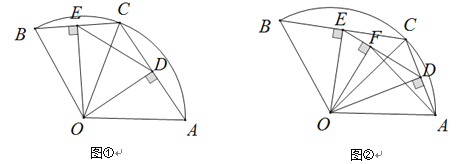
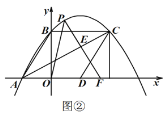
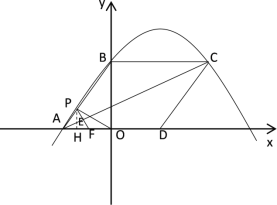
![]() 如图②,延长
如图②,延长![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,若
,若![]() 为等腰三角形,请直接写出点
为等腰三角形,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)最大值为
;(2)最大值为![]() .(3)点P的坐标为
.(3)点P的坐标为![]() 或
或![]()
【解析】
(1)先求出A、B的坐标,然后根据菱形的性质和勾股定理求出BC,从而求出点C的坐标,然后将点A、B、C的坐标代入二次函数解析式中即可求出结论;
(2)作PH⊥x轴于H,交AC于点G,利用待定系数法求出直线AC的解析式,设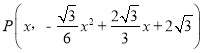 ,则
,则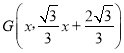 ,从而求出PG与x的函数关系式,然后根据锐角三角函数求出PE与x的函数关系式,然后利用二次函数求最值即可;
,从而求出PG与x的函数关系式,然后根据锐角三角函数求出PE与x的函数关系式,然后利用二次函数求最值即可;
(3)根据点P在BC上方的抛物线上和在AB上方的抛物线上分类讨论,分别画出对应的图形,设出点P的坐标,利用等腰三角形的性质、锐角三角函数列出一元二次方程,即可求出结论.
(1)∵当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
∴![]() ,
,
∵四边形ABCD为菱形
∴![]() ,
,
∴![]()
∴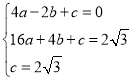 ,
,
解得:![]()
∴抛物线的解析式为:![]() ;
;
(2)作PH⊥x轴于H,交AC于点G,
设直线AC为:![]() ,
,
∴ ,
,
解得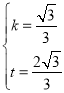 ,
,
∴![]() .
.
设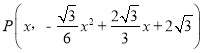 ,则
,则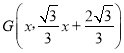 ,
,
∴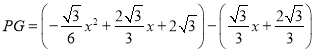 =
=![]()
∵![]() ,
,
∴∠BAO=60°,
∵四边形ABCD为菱形,
∴∠CAD=30°,
∴∠PGE=∠AGH=60°,
∴![]() ,
,
∴![]() =
=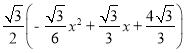 =
=![]() =
=![]() ,
,
∵![]() ,
,
∴当![]() 时,
时,![]() 最大,最大值为
最大,最大值为![]() .
.
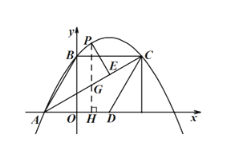
(3)①当点P在BC上方的抛物线上时,作PH⊥x轴于H,
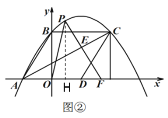
由(2)知∠CAD=30°,
∵PE⊥AC
∴∠PFO=90°-∠CAD=60°
∵△OPF为等腰三角形
∴△OPF为等边三角形
∴∠POH=60°
∴PH=OH·tan∠POH=![]()
设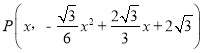 ,则PH=
,则PH=![]() ,OH=x
,OH=x
∴![]()
解得:![]() (不符合前提条件,舍去)
(不符合前提条件,舍去)
∴此时点P的坐标为![]() ;
;
②当点P在AB上方的抛物线上时,作PH⊥x轴于H,
由(2)知∠CAD=30°,
∵PE⊥AC
∴∠PFA=90°-∠CAD=60°
∴∠PFO=120°
∴等腰三角形OPF中,FO=FP
∴∠FOP=∠FPO=![]() ∠PFA=30°
∠PFA=30°
在Rt△OPH中, PH=OH·tan∠POH=![]()
设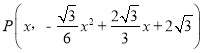 (x<0),则PH=
(x<0),则PH=![]() ,OH=-x
,OH=-x
∴![]()
解得:![]() (不符合前提条件,舍去)
(不符合前提条件,舍去)
∴此时点P的坐标为![]() ;
;
综上:点P的坐标为![]() 或
或![]() .
.

【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制成如下统计图表(单位:cm):
A | x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | x≥170 |
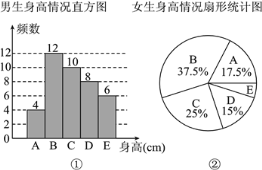
根据图表提供的信息,样本中,身高在160≤x<170之间的女生人数为( )
A. 8 B. 6 C. 14 D. 16