ЬтФПФкШн
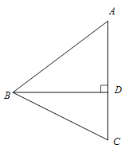
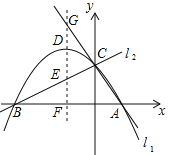
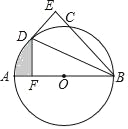
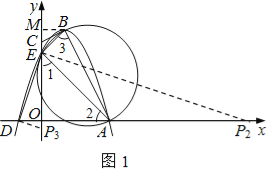
ЁОЬтФПЁПШчЭММзЃЌЫФБпаЮOABCЕФБпOAЁЂOCЗжБ№дкxжсЁЂyжсЕФе§АыжсЩЯЃЌЖЅЕудкBЕуЕФХзЮяЯпНЛxжсгкЕуAЁЂDЃЌНЛyжсгкЕуEЃЌСЌНгABЁЂAEЁЂBEЃЎвбжЊtanЁЯCBE=![]() ЃЌAЃЈ3ЃЌ0ЃЉЃЌDЃЈЉ1ЃЌ0ЃЉЃЌEЃЈ0ЃЌ3ЃЉЃЎ
ЃЌAЃЈ3ЃЌ0ЃЉЃЌDЃЈЉ1ЃЌ0ЃЉЃЌEЃЈ0ЃЌ3ЃЉЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНМАЖЅЕуBЕФзјБъЃЛ
ЃЈ2ЃЉЧѓжЄЃКCBЪЧЁїABEЭтНгдВЕФЧаЯпЃЛ
ЃЈ3ЃЉЪдЬНОПзјБъжсЩЯЪЧЗёДцдквЛЕуPЃЌЪЙвдDЁЂEЁЂPЮЊЖЅЕуЕФШ§НЧаЮгыЁїABEЯрЫЦЃЌШєДцдкЃЌжБНгаДГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ4ЃЉЩшЁїAOEбиxжсе§ЗНЯђЦНвЦtИіЕЅЮЛГЄЖШЃЈ0ЃМtЁм3ЃЉЪБЃЌЁїAOEгыЁїABEжиЕўВПЗжЕФУцЛ§ЮЊsЃЌЧѓsгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂжИГіtЕФШЁжЕЗЖЮЇЃЎ
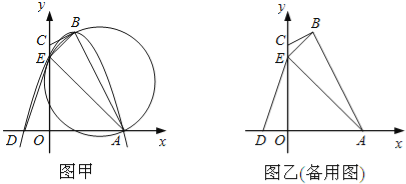
ЁОД№АИЁПЃЈ1ЃЉy=aЃЈxЉ3ЃЉЃЈx+1ЃЉЃЛЕуBЃЈ1ЃЌ4ЃЉ
ЃЈ2ЃЉМћНтЮі
ЃЈ3ЃЉМћНтЮі
ЃЈ4ЃЉs=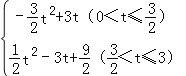
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬтвтЃЌЩшХзЮяЯпНтЮіЪНЮЊy=aЃЈxЉ3ЃЉЃЈx+1ЃЉЃЎ
НЋEЃЈ0ЃЌ3ЃЉДњШыЩЯЪНЃЌНтЕУЃКa=Љ1ЃЎ
Ёрy=Љx2+2x+3ЃЎ
дђЕуBЃЈ1ЃЌ4ЃЉЃЎ
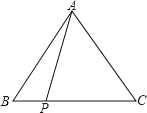
ЃЈ2ЃЉжЄУїЃКШчЭМ1ЃЌЙ§ЕуBзїBMЁЭyгкЕуMЃЌдђMЃЈ0ЃЌ4ЃЉЃЎ
дкRtЁїAOEжаЃЌOA=OE=3ЃЌ
ЁрЁЯ1=ЁЯ2=45ЁуЃЌAE=![]() =3
=3![]() ЃЎ
ЃЎ
дкRtЁїEMBжаЃЌEM=OMЉOE=1=BMЃЌ
ЁрЁЯMEB=ЁЯMBE=45ЁуЃЌBE=![]() =
=![]() ЃЎ
ЃЎ
ЁрЁЯBEA=180ЁуЉЁЯ1ЉЁЯMEB=90ЁуЃЎ
ЁрABЪЧЁїABEЭтНгдВЕФжБОЖЃЎ
дкRtЁїABEжаЃЌtanЁЯBAE=![]() =
=![]() =tanЁЯCBEЃЌ
=tanЁЯCBEЃЌ
ЁрЁЯBAE=ЁЯCBEЃЎ
дкRtЁїABEжаЃЌЁЯBAE+ЁЯ3=90ЁуЃЌЁрЁЯCBE+ЁЯ3=90ЁуЃЎ
ЁрЁЯCBA=90ЁуЃЌМДCBЁЭABЃЎ
ЁрCBЪЧЁїABEЭтНгдВЕФЧаЯпЃЎ
ЃЈ3ЃЉНтЃКRtЁїABEжаЃЌЁЯAEB=90ЁуЃЌtanЁЯBAE=![]() ЃЌsinЁЯBAE=
ЃЌsinЁЯBAE=![]() ЃЌcosЁЯBAE=
ЃЌcosЁЯBAE=![]() ЃЛ
ЃЛ
ШєвдDЁЂEЁЂPЮЊЖЅЕуЕФШ§НЧаЮгыЁїABEЯрЫЦЃЌдђЁїDEPБиЮЊжБНЧШ§НЧаЮЃЛ
ЂйDEЮЊаББпЪБЃЌP1дкxжсЩЯЃЌДЫЪБP1гыOжиКЯЃЛ
гЩDЃЈЉ1ЃЌ0ЃЉЁЂEЃЈ0ЃЌ3ЃЉЃЌЕУOD=1ЁЂOE=3ЃЌМДtanЁЯDEO=![]() =tanЁЯBAEЃЌМДЁЯDEO=ЁЯBAE
=tanЁЯBAEЃЌМДЁЯDEO=ЁЯBAE
ТњзуЁїDEOЁзЁїBAEЕФЬѕМўЃЌвђДЫ OЕуЪЧЗћКЯЬѕМўЕФP1ЕуЃЌзјБъЮЊЃЈ0ЃЌ0ЃЉЃЎ
ЂкDEЮЊЖЬжБНЧБпЪБЃЌP2дкxжсЩЯЃЛ
ШєвдDЁЂEЁЂPЮЊЖЅЕуЕФШ§НЧаЮгыЁїABEЯрЫЦЃЌдђЁЯDEP2=ЁЯAEB=90ЁуЃЌsinЁЯDP2E=sinЁЯBAE=![]() ЃЛ
ЃЛ
ЖјDE=![]() =
=![]() ЃЌдђDP2=DEЁТsinЁЯDP2E=
ЃЌдђDP2=DEЁТsinЁЯDP2E=![]() ЁТ
ЁТ![]() =10ЃЌOP2=DP2ЉOD=9
=10ЃЌOP2=DP2ЉOD=9
МДЃКP2ЃЈ9ЃЌ0ЃЉЃЛ
ЂлDEЮЊГЄжБНЧБпЪБЃЌЕуP3дкyжсЩЯЃЛ
ШєвдDЁЂEЁЂPЮЊЖЅЕуЕФШ§НЧаЮгыЁїABEЯрЫЦЃЌдђЁЯEDP3=ЁЯAEB=90ЁуЃЌcosЁЯDEP3=cosЁЯBAE=![]() ЃЛ
ЃЛ
дђEP3=DEЁТcosЁЯDEP3=![]() ЁТ
ЁТ![]() =
=![]() ЃЌOP3=EP3ЉOE=
ЃЌOP3=EP3ЉOE=![]() ЃЛ
ЃЛ
злЩЯЃЌЕУЃКP1ЃЈ0ЃЌ0ЃЉЃЌP2ЃЈ9ЃЌ0ЃЉЃЌP3ЃЈ0ЃЌЉ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ4ЃЉНтЃКЩшжБЯпABЕФНтЮіЪНЮЊy=kx+bЃЎ
НЋAЃЈ3ЃЌ0ЃЉЃЌBЃЈ1ЃЌ4ЃЉДњШыЃЌЕУ![]() НтЕУ
НтЕУ![]()
Ёрy=Љ2x+6ЃЎ
Й§ЕуEзїЩфЯпEFЁЮxжсНЛABгкЕуFЃЌЕБy=3ЪБЃЌЕУx=![]() ЃЌЁрFЃЈ
ЃЌЁрFЃЈ![]() ЃЌ3ЃЉЃЎ
ЃЌ3ЃЉЃЎ
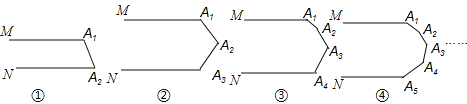
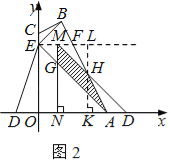
ЧщПівЛЃКШчЭМ2ЃЌЕБ0ЃМtЁм![]() ЪБЃЌЩшЁїAOEЦНвЦЕНЁїDNMЕФЮЛжУЃЌMDНЛABгкЕуHЃЌMNНЛAEгкЕуGЃЎ
ЪБЃЌЩшЁїAOEЦНвЦЕНЁїDNMЕФЮЛжУЃЌMDНЛABгкЕуHЃЌMNНЛAEгкЕуGЃЎ
дђON=AD=tЃЌЙ§ЕуHзїLKЁЭxжсгкЕуKЃЌНЛEFгкЕуLЃЎ
гЩЁїAHDЁзЁїFHMЃЌЕУ![]() ЃЌМД
ЃЌМД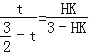 ЃЎ
ЃЎ
НтЕУHK=2tЃЎ
ЁрSвѕ=SЁїMNDЉSЁїGNAЉSЁїHAD=![]() ЁС3ЁС3Љ
ЁС3ЁС3Љ![]() ЃЈ3ЉtЃЉ2Љ
ЃЈ3ЉtЃЉ2Љ![]() t2t=Љ
t2t=Љ![]() t2+3tЃЎ
t2+3tЃЎ
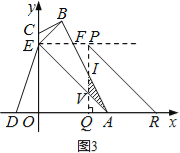
ЧщПіЖўЃКШчЭМ3ЃЌЕБ![]() ЃМtЁм3ЪБЃЌЩшЁїAOEЦНвЦЕНЁїPQRЕФЮЛжУЃЌPQНЛABгкЕуIЃЌНЛAEгкЕуVЃЎ
ЃМtЁм3ЪБЃЌЩшЁїAOEЦНвЦЕНЁїPQRЕФЮЛжУЃЌPQНЛABгкЕуIЃЌНЛAEгкЕуVЃЎ
гЩЁїIQAЁзЁїIPFЃЌЕУ![]() ЃЎМД
ЃЎМД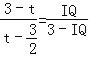 ЃЌ
ЃЌ
НтЕУIQ=2ЃЈ3ЉtЃЉЃЎ
ЁрSвѕ=SЁїIQAЉSЁїVQA=![]() ЁСЃЈ3ЉtЃЉЁС2ЃЈ3ЉtЃЉЉ
ЁСЃЈ3ЉtЃЉЁС2ЃЈ3ЉtЃЉЉ![]() ЃЈ3ЉtЃЉ2=
ЃЈ3ЉtЃЉ2=![]() ЃЈ3ЉtЃЉ2=
ЃЈ3ЉtЃЉ2=![]() t2Љ3t+
t2Љ3t+![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃКs=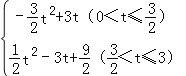 ЃЎ
ЃЎ

 бєЙтПЮЬУПЮЪБзївЕЯЕСаД№АИ
бєЙтПЮЬУПЮЪБзївЕЯЕСаД№АИ гЅХЩНЬИЈЯЮНгНЬВФКгББНЬг§ГіАцЩчЯЕСаД№АИ
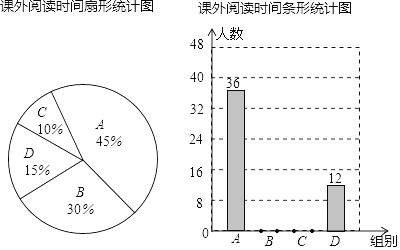
гЅХЩНЬИЈЯЮНгНЬВФКгББНЬг§ГіАцЩчЯЕСаД№АИЁОЬтФПЁПЮЊСЫДДНЈЪщЯуаЃдАЃЌЧаЪЕв§ЕМбЇЩњЖрЖСЪщЃЌЖСКУЪщЃЎФГжабЇПЊеЙСЫЁАКУЪщАщЮвГЩГЄЁБЕФЖСЪщНкЛюЖЏЃЌЮЊСЫСЫНтБОаЃбЇЩњУПжмПЮЭтдФЖСЪБМфЃЌЫцЛњГщШЁВПЗжбЇЩњНјааЮЪОэЕїВщЃЌНЋПЮЭтдФЖСЪБМфЗжЮЊAЁЂBЁЂCЁЂDЫФзщЃЌВЂРћгУГєбѕЫљЕУЕФЪ§ОнЛцжЦСЫШчЯТЭГМЦЭМЃЎ
зщБ№ | ПЮЭтдФЖСtЃЈЕЅЮЛЃКЪБЃЉ |
A | XЃМ2 |
B | 2ЁмxЃМ3 |
C | 3ЁмxЃМ4 |
D | xЁн4 |
ЧыИљОнЭМжаЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉвЛЙВЕїВщСЫ________УћбЇЩњЃЛ
ЃЈ2ЃЉЩШаЮЭГМЦЭМжаAзщЕФдВаФНЧЖШЪ§________ЃЛ
ЃЈ3ЃЉжБНгВЙШЋЬѕаЮЭГМЦЭМ
ЃЈ4ЃЉШєИУаЃга2400УћбЇЩњЃЌИљОнФуЫљЕїВщЕФНсЙћЃЌЙРМЦУПжмПЮЭтдФЖСЪБМфВЛзу3аЁЪБЕФбЇЩњгаЖрЩйШЫЃП