题目内容
【题目】如图,在四边形ABCD中,∠A=∠C=90°,∠ABC,∠ADC的平分线分别与AD,BC相交于E,F两点,FG⊥BE于点G,∠1与∠2之间有怎样的数量关系?为什么?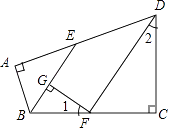
【答案】解:∠1=∠2,
理由:∵∠A=∠C=90°,根据四边形的内角和得,∠ADC+∠ABC=180°,
∵BE平分∠ABC,DF平分∠ADC,
∴∠EBC= ![]() ∠ABC,∠2=
∠ABC,∠2= ![]() ∠ADC,
∠ADC,
∴∠EBC+∠2= ![]() ∠ABC+
∠ABC+ ![]() ∠ADC=90°,
∠ADC=90°,
∵FG⊥BE,
∴∠FGB=90°,
∴∠1+∠EBC=90°,
∴∠1=∠2
【解析】先根据四边形的内角和求出∠ADC+∠ABC=180°,再结合角平分线得出∠EBC+∠2=90°,再利用直角三角形的两锐角互余得出,∠1+∠EBC=90°,即可得出结论.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目