题目内容
【题目】如图,BE是△ABC的角平分线,点D是AB边上一点,且∠DEB=∠DBE. 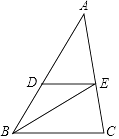
(1)DE与BC平行吗?为什么?
(2)若∠A=40°,∠ADE=60°,求∠C的度数.
【答案】
(1)解:DE∥BC.
理由如下:∵BE是△ABC的角平分线,
∴∠DBE=∠EBC,
∵∠DEB=∠DBE,
∴∠DEB=∠EBC,
∴DE∥BC
(2)解:∵DE∥BC,
∴∠ABC=∠ADE,
∵∠ADE=60°,
∴∠ABC=60°,
在△ABC中,∠A+∠ABC+∠C=180°,
∴∠C=180°﹣∠A﹣∠ABC=180°﹣40°﹣60°=80°
【解析】(1)根据角平分线的定义可得∠DBE=∠EBC,从而求出∠DEB=∠EBC,再利用内错角相等,两直线平行证明即可;(2)根据两直线平行,同位角相等可得∠ABC=∠ADE,再利用三角形的内角和等于180°列式计算即可得解.
【考点精析】解答此题的关键在于理解平行线的判定的相关知识,掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,以及对三角形的内角和外角的理解,了解三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目