Question

【题目】已知，在平面直角坐标系xOy中，点A的坐标为(0，2)，点P(m，n)是抛物线上的一个动点.

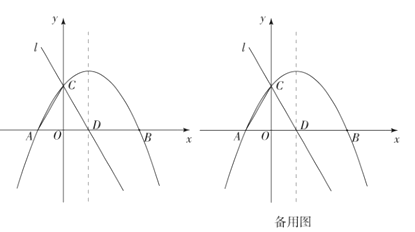
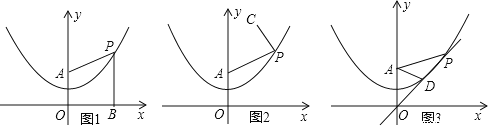
(1)如图1，过动点P作PB⊥x轴，垂足为B，连接PA，请通过测量或计算，比较PA与PB的大小关系：PA_____PB(直接填写“＞”“＜”或“=”，不需解题过程)；

(2)请利用(1)的结论解决下列问题：

①如图2，设C的坐标为(2，5)，连接PC，AP+PC是否存在最小值？如果存在，求点P的坐标；如果不存在，简单说明理由；

②如图3，过动点P和原点O作直线交抛物线于另一点D，若AP=2AD，求直线OP的解析式.

Answer 1

【答案】(1)=；(2)①存在，P(2，2)；②

【解析】

（1）运用二次函数的性质，两点距离公式

（2）①由于PA相当于P到X轴的距离，所以AP+PC最小值，应为直线距离最小.

②过点D,点P，分别作X轴的垂线，垂足为E,F,通过AP=2AD联立方程可求得.

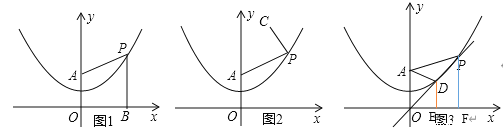
解（1）设

∵

，∴

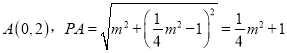（2）①∵P为抛物线上的动点，由上述结论PA距离即为P到X轴的距离，因此AP+PC最小值应为直线距离，过点C到X轴的距离，交抛物线于P,点P的横坐标为2，所以纵坐标为 ，即P(2，2)

②解：∵ ∴

设 又过直线OP正比例图像

∴

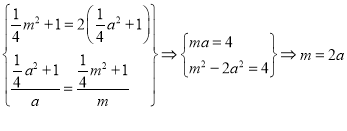
得到 所以 ,则OP的解析式.