题目内容
【题目】如图,已知![]() 和
和![]() 均为的等边三角形,点
均为的等边三角形,点![]() 为
为![]() 的中点,过点
的中点,过点![]() 与
与![]() 平行的直线交射线
平行的直线交射线![]() 于点
于点![]() .
.
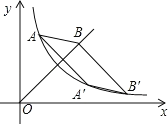
(1)当![]() ,
,![]() ,
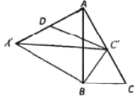
,![]() 三点在同一直线上时(如图1),求证:
三点在同一直线上时(如图1),求证:![]() 为
为![]() 中点;
中点;
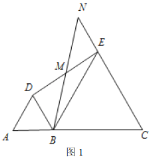
(2)将图1中的![]() 绕点
绕点![]() 旋转,当
旋转,当![]() ,
,![]() ,
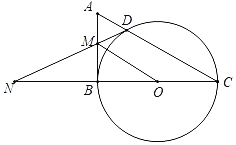
,![]() 三点在同一直线上时(如图2),求证:
三点在同一直线上时(如图2),求证:![]() 为等边三角形;
为等边三角形;
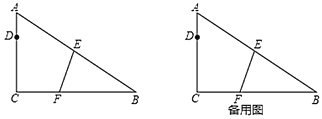
(3)将图2中![]() 绕点
绕点![]() 继续顺时针旋转多少度时,点
继续顺时针旋转多少度时,点![]() 恰好第一次位于线段
恰好第一次位于线段![]() 中点,试作出图形并直接写出
中点,试作出图形并直接写出![]() 绕点
绕点![]() 继续旋转的度数.
继续旋转的度数.
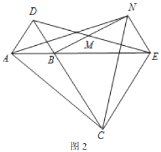
【答案】(1)见解析;(2)见解析;(3)![]() 绕点
绕点![]() 继续顺时针旋转30度时,点
继续顺时针旋转30度时,点![]() 恰好第一次位于线段
恰好第一次位于线段![]() 中点
中点
【解析】
(1) 根据![]() ,点
,点![]() 为
为![]() 的中点,可证明
的中点,可证明![]() ,从而
,从而![]() ,可得到答案;
,可得到答案;
(2) 先证明![]() ,得到
,得到![]() ,再证
,再证![]() 由一个角是60°,即证明
由一个角是60°,即证明![]() 是等边三角形;
是等边三角形;
(3) 先证明![]() ,证
,证![]() ,得到
,得到![]() 是等边三角形,再利用点
是等边三角形,再利用点![]() 恰好第一次位于线段
恰好第一次位于线段![]() 中点,可得到答案.
中点,可得到答案.
证明:(1)∵![]() ,
,
∴![]() ,
,![]() ,
,
∵点![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
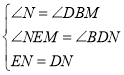
∴![]() ,
,
∴![]() ,即
,即![]() 为
为![]() 中点.
中点.
(2)∵![]() ,
,
∴![]() ,(1)中已经证明,
,(1)中已经证明,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() 三点在同一直线上,
三点在同一直线上,
∴![]() ,
,
∵![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
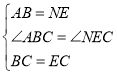
∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() 为等边三角形(由一个角是60°的等腰三角形是等边三角形).
为等边三角形(由一个角是60°的等腰三角形是等边三角形).
(3)如图,当![]() 绕点
绕点![]() 继续旋转时,点
继续旋转时,点![]() 在线段
在线段![]() 上.
上.
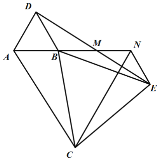
![]() 绕点
绕点![]() 继续旋转30度时,点
继续旋转30度时,点![]() 恰好第一次位于线段
恰好第一次位于线段![]() 中点.
中点.
(附理由:∵![]() ,
,
∴![]() (1)中已经证明,
(1)中已经证明,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() 为等边三角形.
为等边三角形.
∴当点![]() 恰好位于线段
恰好位于线段![]() 中点时,
中点时,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
即![]() 绕点
绕点![]() 继续顺时针旋转30度时,点
继续顺时针旋转30度时,点![]() 恰好第一次位于线段
恰好第一次位于线段![]() 中点.
中点.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目