题目内容
【题目】已知抛物线
与
轴交于
、
两点(点在点的左侧)，与
轴交于点
，顶点为
．
（1）请求出、两点的坐标；
（2）将抛物线绕平面内的某一点旋转180°，旋转后得到抛物线
，抛物线的顶点为
，与轴相交于
、
两点(点
在点的右侧)，使得抛物线过点，且以点、、、为顶点的四边形为平行四边形，请求出所有满足条件的抛物线的顶点坐标．
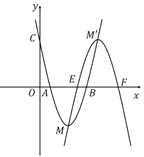
【答案】（1）
、
；（2）
、
【解析】
（1）将x＝0代入即可求得点C坐标，将函数关系式配成顶点式即可求得点M的坐标；
（2）先根据中心对称可得点
在抛物线
的图像上，当点抛物线
对称轴的右侧时，过点M作MG⊥y轴于点G，过点作M'G⊥x轴于点H，根据平行四边形的性质可得CM∥M'F，CM＝M'F，进而可证得△CGM≌△M'HF，从而可得点M'的纵坐标，代入抛物线即可求得点M'的坐标，当点抛物线对称轴的左侧时，同理可得．
解：（1）当x＝0时，y＝5，则点C坐标为（0,5），
∵
，
∴顶点M的坐标为（3，－4），
（2）∵抛物线绕平面内的某一点旋转180°，旋转后得到抛物线
，
∴与关于该点成中心对称
∵经过的顶点
，
∴经过的顶点，
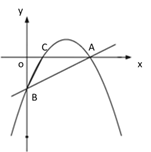
如图，当点抛物线对称轴的右侧时，
过点M作MG⊥y轴于点G，过点作M'G⊥x轴于点H，
当四边形
为平行四边形时，则CM∥M'F，CM＝M'F，
∴△CGM≌△M'HF，
∵点C坐标为（0,5），点M的坐标为（3，－4），
∴M'H＝CG＝5－（－4）＝9，
∴点M'的纵坐标为9，
将y＝9代入
得
，
解得
∴此时点M'的坐标为
，
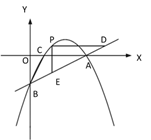
如图，当点抛物线对称轴的左侧时，
同理可得，此时点M'的坐标为
，
综上所述，此时点M'的坐标为或
【题目】为了了解初三学生的中考体育备考情况，西安铁一中分校体育组从初三年级全年级学生中随机抽取部分学生进行测试，现将从报排球项目所有女生中随机抽取到的60名女生的排球成绩(40秒内有效垫球个数)进行整理，得到下列图表中信息：
垫球个数 | 频数 |
|
|
| 4 |
|
|
| 26 |
| 10 |
请根据所给信息，解答下列问题：
（1）
__________，
__________；
（2）这60名学生垫球个数的中位数落在__________段；
（3）全校报考排球项目女生共有450人，根据以往的经验垫球个数在30个以上(包含30个)在中考中能取得良好以上成绩，请估计中考体育考试中女生排球项目达到良好以上的女生人数．
