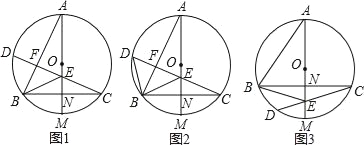
题目内容
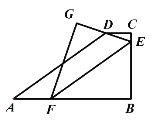
【题目】已知:在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在对角线
在对角线![]() 上(不与点
上(不与点![]() 重合),
重合),![]() ,
,![]() 的延长线与射线
的延长线与射线![]() 交于点
交于点![]() ,设
,设![]() 的长为
的长为![]() .
.
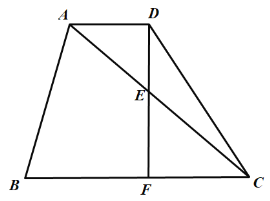
(1)如图,当![]() 时,求
时,求![]() 的长;
的长;
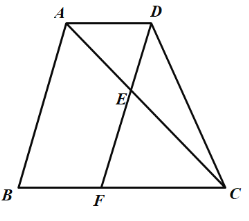
(2)设![]() 的长为
的长为![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并直接写出定义域;
的函数解析式,并直接写出定义域;
(3)当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() (
(![]() 且
且![]() );(3)当
);(3)当![]() 是等腰三角形时,
是等腰三角形时,![]() 的长是6或
的长是6或![]() .
.
【解析】
(1)过![]() 作
作![]() ,利用
,利用![]() 求出CH,根据勾股定理求出AH,再证明四边形
求出CH,根据勾股定理求出AH,再证明四边形![]() 是矩形,得到
是矩形,得到![]() ,再根据
,再根据![]() ,
,![]() 求出
求出![]() ,从而求出AD;
,从而求出AD;
(2)根据题意证明![]() ,得到
,得到![]() ,故
,故![]() ,在
,在![]() 中,利用勾股定理得到
中,利用勾股定理得到![]() 故得到
故得到![]() ,即可得到
,即可得到![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)先证明![]() ,再分DF=DC、FC=DC、FC=FD三种情况,根据y与x的函数关系与三角函数的定义求解即可.
,再分DF=DC、FC=DC、FC=FD三种情况,根据y与x的函数关系与三角函数的定义求解即可.
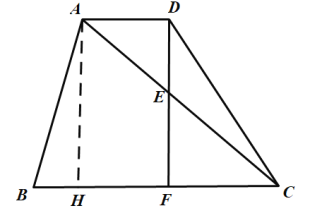
解:(1)过![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
∵在![]() 中,
中,![]() ,且
,且![]() ,
,![]() ,
,
∴![]() .
.
∵在![]() 中,
中,![]() ,
,
∴![]()
∴在![]() 中,
中,![]() ,
,
∵![]() ,且
,且![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴![]()
∵在![]() 中,
中,![]() ,且
,且![]()
∴![]() ,得:
,得:![]()
∴![]()
(2)∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]()
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]()
∵在![]() 中,
中,![]()
∴![]() ,即
,即![]() (
(![]() 且
且![]() )
)
(3)由![]() ,
,![]() 得:
得:![]() ,
,
又![]() 有
有![]() ,
,
∴![]()
∴当![]() 是等腰三角形时,
是等腰三角形时,![]() 也是等腰三角形
也是等腰三角形
∴1°当![]() 时,不存在;
时,不存在;
2°当![]() 时,得:
时,得:![]() ,即
,即![]()
解得:![]() (舍),
(舍),![]()
3°当![]() 时,在
时,在![]() 中由
中由![]()
得: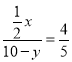 ,解得:
,解得:![]() (舍),
(舍),![]()
∴综上所述,当![]() 是等腰三角形时,
是等腰三角形时,![]() 的长是6或
的长是6或![]() .
.

练习册系列答案
相关题目