题目内容
【题目】如图,点![]() 为
为![]() 轴负半轴上一点,点
轴负半轴上一点,点![]() 为
为![]() 轴正半轴上一点,
轴正半轴上一点,![]() 、
、![]() 的长分别是关于
的长分别是关于![]() 的一元二次方程
的一元二次方程![]() 的两根,
的两根,![]() ,且
,且![]() ,则
,则![]() 的度数为________.
的度数为________.
【答案】![]()
【解析】
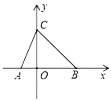
根据三角形AOB面积为6,OC=3,利用三角形面积公式求出AB=4,而AB=OA+OB,利用根与系数的关系求出m的值,确定出OB的长,即可确定出∠ABC的度数.
∵S△ABC=![]() ABOC=6,OC=3,
ABOC=6,OC=3,
∴AB=4,即OA+OB=4,
∵OA,OB(OA<OB)的长分别是关于x的一元二次方程x2-4mx+m2+2=0的两根,
∴OA+OB=4m,即4m=4,
解得:m=1,
代入方程得:x2-4x+3=0,即(x-1)(x-3)=0,
解得:x1=1,x2=3,
∴OA=1,OB=3,
∴OC=OB=3,即△BOC为等腰直角三角形,
∴∠ABC=45°.
故答案为:45°

练习册系列答案
相关题目