Question

【题目】在以“关爱学生、安全第一”为主题的安全教育宣传月活动中，某学校为了了解本校学生的上学方式，在全校范围内随机抽查部分学生，了解到上学方式主要有：A﹣﹣结伴步行、B﹣﹣自行乘车、C﹣﹣家人接送、D﹣﹣其它方式，并将收集的数据整理绘制成如下两幅不完整的统计图，请根据图中信息，解答下列问题：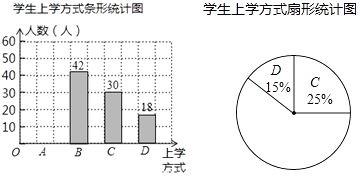

（1）本次抽查的学生人数是多少人？
（2）请补全条形统计图和扇形统计图，并在图中标出“自行乘车”对应扇形的圆心角的度数；
（3）如果该校学生有2080人，请你估计该校“家人接送”上学的学生约有多少人？

Answer 1

【答案】
（1）解：∵30÷25%=120，

∴本次抽查的学生人数是120人；

（2）解：A方式的人数为120﹣（42+30+18）=40，

A方式人数占总人数的百分比为 ×100%=30%，B方式人数占总人数的百分比为 ×100%=35%，

则“自行乘车”对应扇形的圆心角的度数为360°×35%=126°，

补全图形如下：

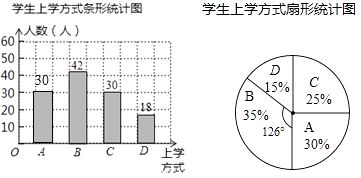
（3）解：2080×25%=520，

答：估计该校“家人接送”上学的学生约有520人．

【解析】（1）要求抽查学生的人数，根据统计图可知，利用D或C的人数和所占的百分比即可求解。
（2）根据A方式的人数=抽查的总人数-B、C、D方式的人数的人数之和。计算即可，再补全条形统计图；先求出B的百分比，再用B所占的百分比乘以360°，即可求出“自行乘车”对应扇形的圆心角的度数。
（3）用该校学生的总人数D所占的百分比，即可求得答案。
【考点精析】根据题目的已知条件，利用扇形统计图和条形统计图的相关知识可以得到问题的答案，需要掌握能清楚地表示出各部分在总体中所占的百分比．但是不能清楚地表示出每个项目的具体数目以及事物的变化情况；能清楚地表示出每个项目的具体数目，但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况．