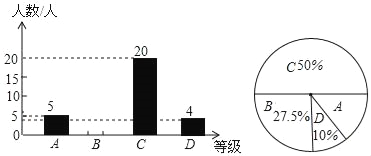
ΧβΡΩΡΎ»ί
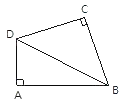
ΓΨΧβΡΩΓΩΡ≥…Χ≥Γ“Σ–όΫ®“ΜΗωΒΊœ¬ΆΘ≥Β≥ΓΘ§ΆΘ≥Β≥ΓΒΡ»κΩΎ…ηΦΤ Ψ“βΆΦ»γΆΦΥυ ΨΘ§Τδ÷––±Τ¬ΒΡ«ψ–±Ϋ«ΈΣ18ΓψΘ§“Μ¬ΞΒΫΒΊœ¬ΆΘ≥Β≥ΓΒΊΟφΒΡΨύάκCDΘΫ2.8ΟΉΘ§“Μ¬ΞΒΫΒΊΤΫœΏΒΡΨύάκBCΘΫ1ΟΉΘ°
(1)ΈΣ±Θ÷Λ–±Τ¬ΒΡ«ψ–±Ϋ«ΈΣ18ΓψΘ§”Π‘ΎΒΊΟφ…œΨύΒψBΕύ‘ΕΒΡA¥ΠΩΣ Φ–±Τ¬ΒΡ ©ΙΛΘΩ(ΫαΙϊΨΪ»ΖΒΫ0.1ΟΉ)
(2)»γΙϊΗχΗΟ…Χ≥ΓΥΆΜθΒΡΜθ≥ΒΗΏΕ»ΈΣ2.5ΟΉΘ§Ρ«Ο¥Α¥’β―υΒΡ…ηΦΤΡήΖώ±Θ÷ΛΜθ≥ΒΥ≥άϊΫχ»κΒΊœ¬ΆΘ≥Β≥ΓΘΩ«κΥΒΟςάμ”…Θ°(≤ΈΩΦ ΐΨίΘΚsin 18ΓψΓ÷0.31Θ§cos 18ΓψΓ÷0.95Θ§tan 18ΓψΓ÷0.32)
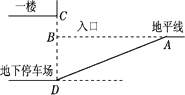
ΓΨ¥πΑΗΓΩΘ®1Θ©5.6ΟΉΘΜΘ®2Θ©ΡήΘ§άμ”…ΦϊΫβΈω
ΓΨΫβΈωΓΩΘ®1Θ©”…Χβ“βΩ…ΒΟΓœBAD=18ΓψΘ§BD=CD-CB=1.8Θ®ΟΉΘ©Θ§»ΜΚσ‘ΎRtΓςABD÷–Θ§”…»ΐΫ«Κ· ΐΒΡ–‘÷ Θ§Φ¥Ω…«σΒΟABΒΡ≥ΛΘΜ
Θ®2Θ© Ήœ»ΙΐCΉςCEΓΆADΘ§¥ΙΉψΈΣEΘ§Ω…«σΒΟΓœDCEΒΡΕ» ΐΘ§»ΜΚσ‘ΎRtΓςCDE÷–Θ§”…»ΐΫ«Κ· ΐΒΡ–‘÷ Φ¥Ω…ΒΟCE=CDcos18ΓψΘ§ΦΧΕχ«σΒΟ¥πΑΗΘ°
ΫβΘΚ(1)”…Χβ“βΩ…ΒΟΓœBADΘΫ18Γψ.‘ΎRtΓςABD÷–Θ§ABΘΫ![]() Γ÷
Γ÷![]() Γ÷5.6(ΟΉ)
Γ÷5.6(ΟΉ)
¥πΘΚ”Π‘ΎΒΊΟφ…œΨύBΒψ5.6ΟΉ‘ΕΒΡA¥ΠΩΣ Φ–±Τ¬ΒΡ ©ΙΛ
(2)Ρή.άμ”…ΘΚ»γΆΦΘ§ΙΐΒψCΉςCEΓΆAD”ΎΒψEΘ§
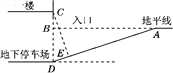
‘ρΓœDCEΘΫΓœBADΘΫ18Γψ.‘ΎRtΓςCED÷–Θ§CEΘΫCDΓΛcos 18ΓψΓ÷2.8ΓΝ0.95ΘΫ2.66(ΟΉ).
ΓΏ2.66ΘΨ2.5Θ§
ΓύΡή±Θ÷ΛΜθ≥ΒΥ≥άϊΫχ»κΒΊœ¬ΆΘ≥Β≥ΓΘ°