题目内容
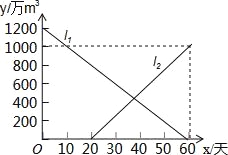
【题目】由于持续高温和连日无雨,某水库的蓄水量随时间的增加而减少,已知原有蓄水量y1(万m3)与干旱持续时间x(天)的关系如图中线段l1所示,针对这种干旱情况,从第20天开始向水库注水,注水量y2(万m3)与时间x(天)的关系如图中线段l2所示(不考虑其它因素).
(1)求原有蓄水量y1(万m3)与时间x(天)的函数关系式,并求当x=20时的水库总蓄水量.
(2)求当0≤x≤60时,水库的总蓄水量y(万m3)与时间x(天)的函数关系式(注明x的范围),若总蓄水量不多于900万m3为严重干旱,直接写出发生严重干旱时x的范围.
【答案】(1)y1=﹣20x+1200,x=20时,y1=800;(2)当0≤x≤20时,y=﹣20x+1200,当20<x≤60时,y=5x+700.
15≤x≤40.
【解析】
试题分析:(1) 根据(0,1200),(60,0)两点求出y1与x的关系式,把x=20代入可求出水库总蓄水量;(2)分两种情况:①当0≤x≤20时,y=y1,②当20<x≤60时,y=y1+y2;并计算分段函数中y≤900时对应的x的取值.
试题解析:(1)设y1=kx+b,把(0,1200)和(60,0)代入到y1=kx+b得:![]() , 解得
, 解得![]() ,
,
∴y1=﹣20x+1200,当x=20时,y1=﹣20×20+1200=800,(2)设y2=kx+b,把(20,0)和(60,1000)代入到y2=kx+b中得:![]() , 解得
, 解得![]() ,∴y2=25x﹣500,当0≤x≤20时,y=﹣20x+1200,
,∴y2=25x﹣500,当0≤x≤20时,y=﹣20x+1200,
当20<x≤60时,y=y1+y2=﹣20x+1200+25x﹣500=5x+700,y≤900,则5x+700≤900,x≤40,
当y1=900时,900=﹣20x+1200,x=15,∴发生严重干旱时x的范围为:15≤x≤40.

 名校课堂系列答案
名校课堂系列答案