题目内容
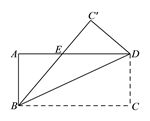
【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在![]() 处,
处,![]() 交AD于点E.
交AD于点E.
(1)试判断△BDE的形状,并说明理由;
(2)若AB=6,![]() ,求△BDE的面积.
,求△BDE的面积.
【答案】(1)等腰三角形,证明见解析;(2)18.75
【解析】试题分析:
(1)由图形折叠前后,对应角相等可得:∠EBD=∠CBD,再由AD∥BC可得∠ADB=∠CBD,从而得到∠EBD=∠ADB,所以BE=DE,即△BDE为等腰三角形;
(2)由图可知,AB是△BDE的边DE上的高,所以只需求出DE的长,就可求△BDE的面积,设DE为x,则BE=DE=x,AE=8-x,在Rt△ABE中,由勾股定理列方程解出x就可求△BDE的面积了.
试题解析:
解:(1)△BDE是等腰三角形.
由折叠可知,∠CBD=∠EBD,
∵AD∥BC,
∴∠CBD=∠EDB,
∴∠EBD=∠EDB,
∴BE=DE,
即△BDE是等腰三角形;
(2)设DE=x,则BE=x,AE=8-x,
在Rt△ABE中,由勾股定理得:AB2+AE2=BE2即62+(8-x)2=x2,
解得:x=5,
所以S△BDE=![]() DE×AB=
DE×AB=![]() ×5×6=18.75.
×5×6=18.75.

练习册系列答案
相关题目
【题目】某校对七年级男生进行俯卧撑测试,以能做8个为达标,超过的次数用正数表示,不足的次数用负数表示,其中10名男生的成绩如下表:
1 | 3 | -1 | 0 | -3 | 4 | 6 | 0 | -2 | -1 |
(1)这10名男生中有几个达标?达标率是百分之几?
(2)这10名男生共做了多少个俯卧撑?