Question

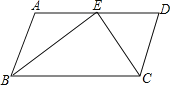
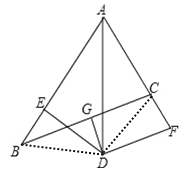
【题目】已知，如图，在△ABC中，AB=8cm，AC=4cm，△BAC的平分线AD与BC的垂直平分线DG交于点D，过点D的直线DE⊥AB于点E，DF⊥AC于点F.

（1）求证：BE=CF；

（2）求AE的长.

Answer 1

【答案】（1）见解析；（2）AE＝6cm.

【解析】

（1）利用角平分线的性质得出DE＝DF，连接BD，CD．利用垂直平分线的性质得出DB＝DC，证得Rt△DCF≌Rt△DBE，得出结论；

（2）易证Rt△AED≌Rt△AFD，可得AE＝AF，结合（1）的结论，利用线段的和与差得出答案即可．

（1）证明：∵点D在∠BAC的平分线上，DE⊥AB，DF⊥AC，

∴DE＝DF．

连接BD，CD．

∵点D在BC的垂直平分线上，

∴DB＝DC；

在Rt△DCF与Rt△DBE中，，

∴Rt△DCF≌Rt△DBE（HL），

∴BE＝CF；

（2）解：∵DE＝DF．

在Rt△AED与Rt△AFD中，，

∴Rt△AED≌Rt△AFD（HL），

∴AE＝AF，

∵AB＝8cm，AC＝4cm，BE＝CF，AE＝AF＝AC＋CF，

∴AB＝AE＋BE＝AC＋BE＋CF＝AC＋2BE，

∴BE＝2cm，

∴AE＝ABBE＝6cm．