题目内容
【题目】如图，已知抛物线y=﹣x2+2x+3与坐标轴交于A，B，C三点，抛物线上的点D与点C关于它的对称轴对称．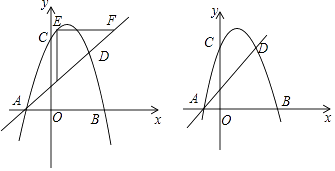
（1）直接写出点D的坐标和直线AD的解析式；
（2）点E是抛物线上位于直线AD上方的动点，过点E分别作EF∥x轴，EG∥y轴并交直线AD于点F、G，求△EFG周长的最大值；
（3）若点P为y轴上的动点，则在抛物线上是否存在点Q，使得以A，D，P，Q为顶点的四边形是平行四边形？若存在，请求出点Q的坐标，若不存在，请说明理由．
【答案】
（1）
解：将x=0代入得y=3，
∴C（0，3）．
∵抛物线的对称轴为x=﹣ 
=1，C（0，3），
∴D（2，3）．
把y=0代入抛物线的解析式得：0=﹣x2+2x+3，解得x=3或x=﹣1，
∴A（﹣1，0）．
设直线AD的解析式为y=kx+b，将点A和点D的坐标代入得： 
，解得：k=1，b=1，
∴直线AD的解析式为y=x+1．
（2）
解：如图1所示：
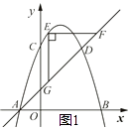
∵直线AD的解析式为y=x+1，
∴∠DAB=45°．
∵EF∥x轴，EG∥y轴，
∴∠GEF=90°，∠GFE=∠DAB=45°
∴△EFG是等腰直角三角形．
∴△EFG的周长=EF+FG+EG=（2+ 
）EG．
依题意，设E（t，﹣t2+2t+3），则G（t，t+1）．
∴EG=﹣t2+2t+3﹣（t+1）=﹣（t﹣ 
）2+ 
．
∴EG的最大值为 ．
∴△EFG的周长的最大值为 
+ 
．
（3）
解：存在．①以AD为平行四边形的边时，PQ∥AD，PQ=AD．
∵A，D两点间的水平距离为3，
∴P，Q两点间的水平距离也为3．
∴点Q的横坐标为3或﹣3．
将x=3和x=﹣3分别代入y=﹣x2+2x+3得y=0或y=﹣12．
∴Q（3，0）或（﹣3，﹣12）．
②当AD为平行四边形的对角线时，设AD的中点为M，
∵A（﹣1，0），D（2，3），M为AD的中点，
∴M（ ， 
）．
设点Q的横坐标为x，则 
= ，解得x=1，
∴点Q的横坐标为1．
将x=1代入y=﹣x2+2x+3得y=4．
∴这时点Q的坐标为（1，4）．
综上所述，当点Q的坐标为Q（3，0）或（﹣3，﹣12）或（1，4）时，以A，D，P，Q为顶点的四边形是平行四边形．
【解析】（1）先求得点C的坐标，然后再求得抛物线的对称轴，由点C与点D关于x=1对称可求得点D的坐标，把y=0代入抛物线的解析式可求得对应的x的值，从而可得到点A的坐标，然后利用待定系数法求得直线AD的解析式即可；（2）首先证明△EFG为等腰直角三角形，则△EFG的周长=（2+ ）EG，设E（t，﹣t2+2t+3），则G（t，t+1），然后得到EG与t的函数关系式，利用配方法可求得EG的最大值，最后依据△EFG的周长=（2+ ）EG求解即可；（3）分为AD为平行四边形的边和AD为平行四边形的对角线时，两种情况，可先利用平行四边形的性质求得点Q的横坐标，然后将点Q的横坐标代入抛物线的解析式可求得点Q的纵坐标．
