题目内容
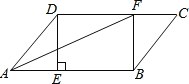
【题目】如图,矩形ABCD中,AB![]() ,BC
,BC![]() ,连结对角线AC,点O为AC的中点,点E为线段BC上的一个动点,连结OE,将△AOE沿OE翻折得到△FOE,EF与AC交于点G,若△EOG的面积等于△ACE的面积的
,连结对角线AC,点O为AC的中点,点E为线段BC上的一个动点,连结OE,将△AOE沿OE翻折得到△FOE,EF与AC交于点G,若△EOG的面积等于△ACE的面积的![]() ,则BE=_____.
,则BE=_____.

【答案】2![]()
【解析】
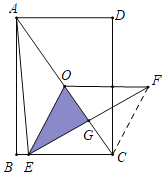
如图,连接CF.想办法证明四边形OECF是平行四边形即可解决问题.
如图,连接CF.
∵OA=OC,△EOG的面积等于△ACE的面积的![]() ,
,
∴OG=GC,
∴OA=2OG,
由翻折不变性可知:∠AEO=∠OEG,
∴![]() 2(角平分线的性质定理,可以用面积法证明),
2(角平分线的性质定理,可以用面积法证明),
∵EA=EF,
∴EG=GF,∵OG=OC,
∴四边形OECF是平行四边形,
∴OF=CE,
∵四边形ABCD是矩形,
∴∠B=90°,
∴AC![]() 2
2![]() ,
,
∴EC=OF=OA![]() ,
,
∴BE=2![]() ,
,
故答案为2![]() .
.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
【题目】4月22日是世界地球日,为了增强学生环保意识,某中学八年级举行了“环保知识竞赛”活动,为了了解本次竞赛情况,只抽取了部分学生的成绩(满分100分,得分均为正整数)进行统计,请你根据下面还未完成的频数分布表和频数分布直方图,解答下列问题:
分组 | 频数 | 频率 |
50.5~60.5 | 4 | 0.08 |
60.5~70.5 | 8 | 0.16 |
70.5~80.5 | 10 | 0.20 |
80.5~90.5 | 16 | 0.32 |
90.5~100.5 | a | b |

(1)a= b= ;
(2)补全频数分布直方图;
(3)该校八年级有500名学生,估计八年级学生中竞赛成绩高于80分的有多少人?