题目内容
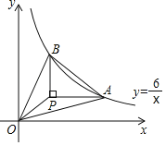
【题目】如图,A、B是函数y=![]() 上两点,P为一动点,作PB∥y轴,PA∥x轴,下列说法:①△AOP≌△BOP;②S△AOP=S△BOP;③若OA=OB,则OP平分∠AOB;④若S△BOP=2,则S△ABP=4,正确有____(填序号)
上两点,P为一动点,作PB∥y轴,PA∥x轴,下列说法:①△AOP≌△BOP;②S△AOP=S△BOP;③若OA=OB,则OP平分∠AOB;④若S△BOP=2,则S△ABP=4,正确有____(填序号)
【答案】②③④
【解析】
由点P是动点,可判断出①错误,设出点P的坐标,求出AP、BP的长,再利用三角形面积公式计算即可判断出②;利用角平分线定理的逆定理可判断③;先求出矩形OMPN=2,进而得出mn=4,最后用三角形的面积公式解答即可.
解:∵点P是动点,
∴BP与AP不一定相等,
∴△BOP与△AOP不一定全等,故①不正确;
设P(m,n),
∵BP∥y轴,
∴B(m, ![]() ),A(
),A(![]() ,n)
,n)
∴AP=|![]() -m|
-m|
∴S△AOP=![]() ·|6-m|n=
·|6-m|n=![]() |6-mn |
|6-mn |
同理:S△BOP=![]() ·|
·|![]() -n|m=
-n|m=![]() |6-mn |
|6-mn |
∴S△AOP=S△BOP;
故②正确;
如图,过点P作PF⊥OA于F,PE⊥OB于E,
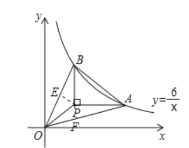
∴S△BOP=![]() OB·PE,S△AOP=
OB·PE,S△AOP=![]() OA·PF
OA·PF
∵S△BOP =S△AOP
∴OB·PE= OA·PF
∵OA=OB,
∴PE=PF,
∵PE⊥OB,PF⊥OA
∴OP是∠AOB的平分线,故③正确;
如图,延长BP交x轴于N,延长AP交轴于M,
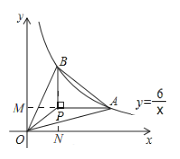
∴AM⊥y轴,BN⊥x轴,
∴四边形OMPN是矩形,
∵点A,B在双曲线y=![]() 上,
上,
∴S△AMO=S△ONB=3,
∵S△BOP=2,
∴S△PMO= S△PNO=1,
∴S矩形OMPN=2,
∴mn=2,
∴m=![]()
∴![]() ,
,![]()
∴![]() 故④正确;
故④正确;
故答案为②③④.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】近年来网约车十分流行,初三某班学生对“美团”和“滴滴”两家网约车公司各10名司机月收入进行了一项抽样调查,司机月收入(单位:千元)如图所示:

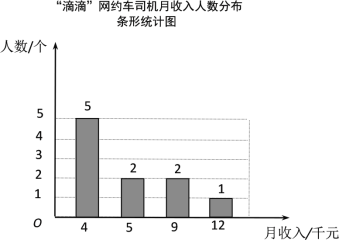
根据以上信息,整理分析数据如下:
平均月收入/千元 | 中位数/千元 | 众数/千元 | 方差/千元2 | |
“美团” | ① | 6 | 6 | 1.2 |
“滴滴” | 6 | ② | 4 | ③ |
(1)完成表格填空;
(2)若从两家公司中选择一家做网约车司机,你会选哪家公司,并说明理由.