Question

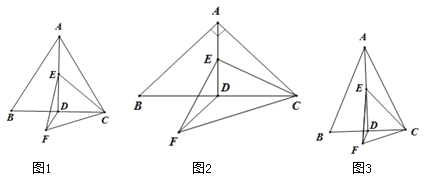
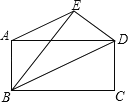
【题目】如图，已知AB=3，BC=4，将矩形ABCD沿对角线BD折叠点C落在点E的位置，则AE的长度为(　　)

A.B.C.3D.

Answer 1

【答案】D

【解析】

利用矩形的性质、折叠的性质，以及勾股定理求出FD，AF的长，再证明△AFE∽△DFB，利用相似三角形的性质即可求解．

解： 设FD=x，则AF=4﹣x，

∵将矩形ABCD沿对角线BD折叠点C落在点E的位置，

∴∠FBD=∠DBC，BE=BC，

∵矩形ABCD，

∴AD∥BC，AD=BC，

∴∠ADB=∠DBC，BE=AD，

∴∠ADB=∠FBD，

∴FB=FD=x，

在直角△AFB中，x2=(4﹣x)2+32，

解之得，x=，AF=4﹣x=，

∵BE=AD，FB=FD，

∴AF=EF，

∴，

∵∠AFE=∠DFB，

∴△AFE∽△DFB，

∴，

∴，

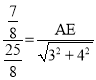解得AE=．

故选：D．