Question

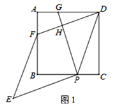
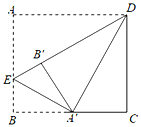
【题目】如图，在矩形ABCD中，AD＝2．将∠A向内翻折，点A落在BC上，记为A′，折痕为DE．若将∠B沿EA′向内翻折，点B恰好落在DE上，记为B′，则AB＝____________．

Answer 1

【答案】

【解析】

证明∠ADE=∠A'DE=∠A'DC=30°，∠C=∠A'B'D=90°，推出△DB'A'≌△DCA'，CD=B'D，设AB=DC=x，在Rt△ADE中，通过勾股定理可求出AB的长度．

∵四边形ABCD为矩形，∴∠ADC＝∠C＝∠B＝90°，AB＝DC，

由翻折知，△AED≌△A'ED，△A'BE≌△A'B'E，∠A'B'E＝∠B＝∠A'B'D＝90°，

∴∠AED＝∠A'ED，∠A'EB＝∠A'EB'，BE＝B'E，

∴∠AED＝∠A'ED＝∠A'EB＝×180°＝60°，

∴∠ADE＝90°﹣∠AED＝30°，∠A'DE＝90°﹣∠A'EB＝30°，

∴∠ADE＝∠A'DE＝∠A'DC＝30°，

又∵∠C＝∠A'B'D＝90°，DA'＝DA'，

∴△DB'A'≌△DCA'（AAS），

∴DC＝DB'，

在Rt△AED中，∠ADE＝30°，AD＝2，

∴AE＝，

设AB＝DC＝x，则BE＝B'E＝x﹣

∵AE2+AD2＝DE2，

∴（）2+22＝（x+x﹣）2，

解得，x1＝（负值舍去），x2＝，

故答案为：．