题目内容
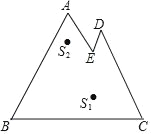
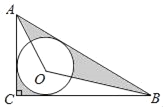
【题目】如图在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，⊙O是△ABC的内切圆，连接AO，BO，则图中阴影部分的面积之和为（ ）
A.10﹣
B.14﹣
πC.12D.14
【答案】B
【解析】
根据勾股定理求出AB，求出△ABC的内切圆的半径，根据扇形面积公式、三角形的面积公式计算，得到答案．
解：设⊙O与△ABC的三边AC、BC、AB的切点分别为D、E、F，连接OD、OE、OF，
在Rt△ABC中，AB＝
＝10，
∴△ABC的内切圆的半径＝
＝2，
∵⊙O是△ABC的内切圆，
∴∠OAB＝
∠CAB，∠OBA＝∠CBA，
∴∠AOB＝180°﹣（∠OAB+∠OBA）＝180°﹣（∠CAB+∠CBA）＝135°，
则图中阴影部分的面积之和＝
，
故选B．
练习册系列答案
发散思维新课堂系列答案
相关题目
