题目内容
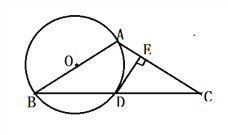
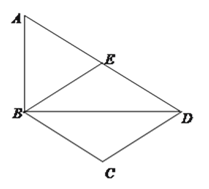
【题目】如图,在Rt△ABD中,∠ABD=90°,AB=1,sin∠ADB=![]() ,点E为AD的中点,线段BA绕点B顺时针旋转到BC(旋转角小于180°),使BC∥AD.连接DC,BE.
,点E为AD的中点,线段BA绕点B顺时针旋转到BC(旋转角小于180°),使BC∥AD.连接DC,BE.
(1)则四边形BCDE是________,并证明你的结论;
(2)求线段AB旋转过程中扫过的面积.
【答案】(1)菱形;(2)![]()
【解析】试题分析:(1)先证四边形BCDE是平行四边形,即可得到结论;
(2)求出∠ABC的度数,根据扇形面积公式计算即可.
试题解析:解:(1)菱形.证明如下:
∵sin∠ADB=![]() ,∴∠ADB=30°,
,∴∠ADB=30°,
在Rt△ABD中,∠ABD=90°,AB=1,∴AD=2。
又点E为AD的中点,∴BE=DE= AB=1,由旋转知BC=1,∴BC=DE,又BC∥AD,∴四边形BCDE是平行四边形,又BE=DE,∴平行四边形BCDE是菱形.
(2)∵BC∥AD,∠ADB=30°,∴∠DBC=30°,∴∠ABC=120°,∴线段AB旋转过程中扫过的面积为![]() =
=![]() .
.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
【题目】某校学生会文艺部换届选举,经初选、复选后,共有甲、乙、丙三人进入最后的竞选.最后决定利用投票的方式对三人进行选举,共发出1800张选票,得票数最高者为当选人,且废票不计入任何一位候选人的得票数内,全校设有四个投票箱,目前第一、第二、第三投票箱已开完所有选票,剩下第四投票箱尚未开箱,结果如表所示(单位:票):
投票箱 | 候选人 | 废票 | 合计 | ||
甲 | 乙 | 丙 | |||
一 | 200 | 211 | 147 | 12 | 570 |
二 | 286 | 85 | 244 | 15 | 630 |
三 | 97 | 41 | 205 | 7 | 350 |
四 | 250 | ||||
下列判断正确的是( )
A. 甲可能当选 B. 乙可能当选 C. 丙一定当选 D. 甲、乙、丙三人都可能当选