Question

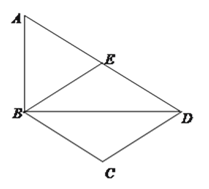
【题目】如图，直角梯形 ABCD 中，AD∥BC，AB⊥BC，AD＝3，BC＝4．将腰 CD 以 D 为旋转中心逆时针旋转 90°至 DE，连结 AE，则△ADE 的面积是（ ）

A.B.2C.D.不能确定

Answer 1

【答案】A

【解析】

作EF⊥AD交AD延长线于点F，作DG⊥BC于点G，首先利用旋转的性质证明△DCG与△DEF全等，再根据全等三角形对应边相等可得EF的长，即△ADE的高，即可求出三角形ADE的面积．

解：如图所示，作EF⊥AD交AD延长线于点F，作DG⊥BC于点G，

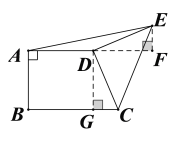
∵CD以D为中心逆时针旋转90°至ED，

∴∠EDF+∠CDF=90°，DE=CD，

又∵∠CDF+∠CDG=90°，

∴∠CDG=∠EDF，

∴△DCG≌△DEF（AAS），

∴EF=CG，

∵AD=3，BC=4，

∴CG=BC－AD=4－3=1，

∴EF=1，

∴△ADE 的面积是.

故选A.