题目内容
【题目】如图，已知∠AOB=75°，∠COD=35°，∠COD在∠AOB的内部绕着点O旋转(OC与OA不重合，OD与OB不重合)，若OE为∠AOC的角平分线．则2∠BOE－∠BOD的值为______．
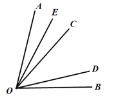
【答案】110°
【解析】
由角平分线的定义可知∠AOC=2∠AOE，由角的和差可知∠BOE=∠AOB-∠AOE，代入2∠BOE－∠BOD整理即可.
∵OE为∠AOC的角平分线，
∴∠AOC=2∠AOE，
∵∠BOE=∠AOB-∠AOE，
∴2∠BOE－∠BOD
=2(∠AOB-∠AOE) －∠BOD
=2∠AOB-2∠AOE －∠BOD
=2∠AOB-∠AOC －∠BOD
=2∠AOB-(∠AOC +∠BOD)
=2∠AOB-(∠AOB -∠COD)
=∠AOB+∠COD
=75°+35°
=110°.
故答案为：110°.
练习册系列答案
阅读快车系列答案
相关题目
