题目内容
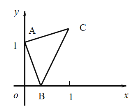
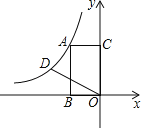
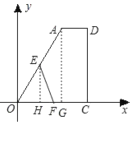
【题目】如图,在四边形![]() 中,O为坐标原点,
中,O为坐标原点,![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() 垂直于
垂直于![]() 轴,
轴,![]() ,
,![]() .若动点
.若动点![]() 、
、![]() 同时从点0出发,
同时从点0出发,![]() 点沿折线
点沿折线![]() 运动,到达
运动,到达![]() 点时停止;
点时停止;![]() 点沿
点沿![]() 运动,到达
运动,到达![]() 点时停止,它们运动的速度都是每秒1个单位长度。设
点时停止,它们运动的速度都是每秒1个单位长度。设![]() 运动
运动![]() 秒时,
秒时,![]() 的面积为
的面积为![]() (平方单位),则
(平方单位),则![]() 关于
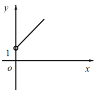
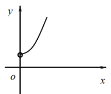
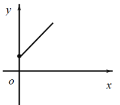
关于![]() 的函数图象大致为( )
的函数图象大致为( )
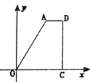
A.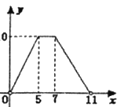 B.
B.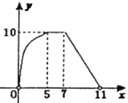
C.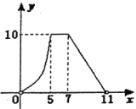
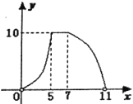
【答案】C
【解析】
首先根据点D的坐标求得点A的坐标,从而求得线段OA和线段OC的长,然后根据运动时间即可判断三角形EOF的面积的变化情况.
解: ∵D(5,4),AD=2.
∴OC=5,CD=4,OA=![]() ,
,
∴运动x秒(x<5) 时,OE=OF=x,
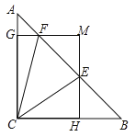
作EH⊥OC于H, AG⊥OC于点G,
∴EH// AG,
∴△EHO∽△AGO,
∴![]() ,
,
即:![]() ,
,
∴EH=![]()
∴S△EOF=![]()
故选项A、B错误;
当点F运动到点C时,点E运动到点A,此时点F停止运动,点E在AD上运动,△EOF的面积不变,
点在DC上运动时,如图,EF=11-x,OC=5
∴S△EOF=![]() ,此函数式是一次函数,故C选项正确,
,此函数式是一次函数,故C选项正确,
故选:C

练习册系列答案
相关题目