题目内容

如图，已知正比例函数和反比例函数的图象都经过点M（-3，-1），且知点P（-1，-精英家教网3）是反比例函数图象上的点：
（1）分别求出正比例函数和反比例函数的解析式；
（2）作PA⊥x轴，垂足为A，当点Q在直线MO上运动时，作QB⊥y轴，垂足为B，问：直线MO上是否存在这样的点Q，使得△OBQ与△OAP面积相等？如果存在，请求出点Q的坐标，如果不存在，请说明理由；
（3）当点Q在第一象限中的双曲线上运动时，作以OP、OQ为邻边的?OPCQ，求?OPCQ周长的最小值以及取得最小值时点Q的坐标．
分析：（1）设正比例函数解析式为y=kx，将点M坐标代入可得k的值，同理代入数据可得反比例函数的关系式，
（2）设点Q的坐标为Q（m，
1
3
m)，由△OBQ与△OAP面积相等，可得关系式，进而可得m的值，代入可得Q1与Q2的坐标；
（3）因为四边形OPCQ是□，所以OP=CQ，OQ=PC，可得P的坐标，设点Q的坐标为Q（n，
3
n
），分析可得求□OPCQ周长的最小值就只需求OQ的最小值，进而可得OQ的二次关系式，解可得答案．
解答：精英家教网解：（1）设正比例函数解析式为y=kx，将点M坐标代入得k=
1
3
，
所以正比例函数解析式为y=
1
3
x；
同样可得，反比例函数解析式为y=
3
x
．

（2）当点Q在直线MO上运动时，设点Q的坐标为Q（m，
1
3
m），
由S△OBQ=
1
2
|OB•BQ|=
1
2
×|
1
3
m•m|=
1
6
m2，
而S△OAP=
1
2
×1×3=
3
2
，
∴
1
6
m2=
3
2
，解得：m=±3，所以点Q的坐标为Q1（3，1）和Q2（-3，-1）．

（3）因为四边形OPCQ是?，所以OP=CQ，OQ=PC，
∵P（-1，-3）是定点，OP是定长，所以求?OPCQ周长的最小值就只需求OQ的最小值．
因为点Q在第一象限中双曲线上，所以可设点Q的坐标为Q（n，
3
n
），
由勾股定理可得：OQ2=n2+
9
n2
．
配方得OQ2=(n-
3
n
)2+6，当n=
3
n
即n=±
3
时，OQ2有最小值6，这时Q（
3
，
3
），
又因为OQ为正值，所以OQ有最小值
6
．
由勾股定理得OP=
10
，所以平行四边形OPCQ周长的最小值是2(
10
+
6
)．
点评：本题考查了反比例函数的图象的性质以及其与直线的关系，利用形数结合解决此类问题，是非常有效的方法．
练习册系列答案
相关题目
如图，已知正比例函数和反比例函数的图象都经过点A（3，3）．
（1）求正比例函数和反比例函数的解析式；
（2）把直线OA向下平移后与反比例函数的图象交于点B（6，m），求m的值和这个一次函数的解析式；
（3）第（2）问中的一次函数的图象与x轴、y轴分别交于C、D，求过A、B、D三点的二次函数的解析式；
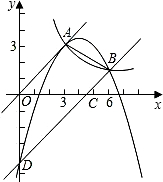（4）在第（3）问的条件下，二次函数在第一象限的图象上是否存在点E，使四边形OECD的面积S1与四精英家教网边形OABD的面积S满足：S1=
23
S？若存在，求点E的坐标；若不存在，请说明理由．
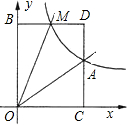精英家教网如图，已知正比例函数y=ax与反比例函数y=
kx
的图象交于点A（3，2）
（1）求上述两函数的表达式；
（2）M（m，n）是反比例函数图象上的一个动点，其中0＜m＜3，过点M作直线MB∥x轴，交y轴于点B；过点A点作直线AC∥y轴交x轴于点C，交直线MB于点D．若s四边形OADM=6，求点M的坐标，并判断线段BM与DM的大小关系，说明理由；
（3）探索：x轴上是否存在点P．使△OAP是等腰三角形？若存在，求出点P的坐标； 若不存在，说明理由．
如图，已知正比例函数y=3x与反比例函数y=
kx
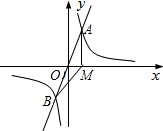(k≠0)的图象都经过点A和点B，点A的横坐精英家教网标为1，过点A作x轴的垂线，垂足为M，连接BM．
求：（1）这个反比例函数的解析式；
（2）△ABM的面积．
精英家教网如图，已知正比例函数y=kx的图象经过点A（-2
3
，a），过点A作AB⊥x轴于点B，△A0B的面积为4
3
．
（1）求k和a的值；
（2）若一次函数y=nx+2的图象经过点A，并且与X轴相交于点M，问：在x轴上是否存在点P，使得以三点P、A、M组成的三角形AMP为等腰三角形？如果存在，请求出点P的坐标；如果不存在，请说明理由．
精英家教网如图，已知正比例函数和反比例函数的图象都经过点A（3，3）．
（1）求正比例函数和反比例函数的解析式；
（2）把直线OA向下平移后与反比例函数的图象交于点B（6，m），求m的值和这个一次函数的解析式；
（3）第（2）问中的一次函数的图象与x轴、y轴分别交于C、D，求过A、B、D三点的三角形的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网